Cho tam giác ABC vuông tạiA ,AB=3cm, AC=4cm
a)Giải tam giác vuông BC
b)Kẻ đường cao AH,tính AH,HB,HC
c)Từ H kẻ HM và HN lần lượt vuông góc vời HB và AC.Chứng minh AM.AB=AN.AC
d)Gọi E là trung điểm BC.Chứng minh AE vuông góc với MN
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
2 tháng 9 2017
tự vẽ hình nha bn
a. Ta có: \(BC=\sqrt{AB^2+AC^2}=\sqrt{3^2+4^2}=5\)(Theo định lí Pytago, tam giác ABC vuông tại A)
b. Ta có: \(\frac{BH}{CH}=\frac{3}{4}\)
\(\Leftrightarrow\frac{BH+CH}{CH}=\frac{3}{4}+1\)
\(\Leftrightarrow\frac{BC}{CH}=\frac{7}{4}\)\(\Leftrightarrow\frac{5}{CH}=\frac{7}{4}\)\(\Leftrightarrow CH=\frac{5.4}{7}=\frac{20}{7}\)
\(\Rightarrow BH=5-\frac{20}{7}=\frac{15}{7}\)
8 tháng 3 2022
a.Xét tam giác ANH và tam giác AHC, có:
\(\widehat{ANH}=\widehat{AHC}=90^0\)
\(\widehat{NAH}=\widehat{HCA}\) ( cùng phụ với \(\widehat{A}\) )
Vậy tam giác ANH đồng dạng tam giác AHC ( g.g )
b. Xét tam giác AHB và tam giác ABC, có:
\(\widehat{BAC}=\widehat{AHB}=90^0\)
\(\widehat{B}:chung\)
Vậy tam giác AHB đồng dạng tam giác ABC ( g.g )
\(\Rightarrow\dfrac{AH}{AC}=\dfrac{BH}{AB}\)
\(\Leftrightarrow\dfrac{12}{13}=\dfrac{BH}{15}\)
\(\Leftrightarrow13BH=180\)
\(\Leftrightarrow BH=\dfrac{180}{13}cm\)
Xét tam giác AHC và tam giác ABC, có:
\(\widehat{CAB}=\widehat{CHA}=90^0\)
\(\widehat{C}:chung\)
Vậy tam giác AHC đồng dạng tam giác ABC ( g.g )
\(\Rightarrow\dfrac{AH}{AB}=\dfrac{CH}{AC}\)
\(\Leftrightarrow\dfrac{12}{15}=\dfrac{CH}{13}\) \(\Leftrightarrow\dfrac{4}{5}=\dfrac{CH}{13}\)
\(\Leftrightarrow5CH=52\)
\(\Leftrightarrow CH=\dfrac{52}{5}cm\)
28 tháng 6 2023
Sửa đề: ΔABC vuông tại A
a: MB/NH=BH^2/AB:CH^2/AC
=BH^2/CH^2*AC/AB
=(AB/AC)^4*AC/AB=AB^3/AC^3
b: BC*BM*CN
=BC*BH^2/AB*CH^2/AC
=AH^4/AH=AH^3
c: ΔAHB vuông tại H có HM là đường cao
nên AM*AB=AH^2
ΔAHC vuông tại H có HN là đường cao
nen AN*AC=AH^2
ΔABC vuông tại A có AH vuông góc BC
nên HB*HC=AH^2
=>HB*HC=AM*AB
góc AMH=góc ANH=góc MAN=90 độ
=>AMHN là hình chữ nhật
=>AH=MN
=>AM*AB=HB*HC=MN^2
d: BM*BA+AN*AC
=BH^2+AH^2=AB^2=BH*BC
28 tháng 12 2020
a) Xét tứ giác AMHN có
\(\widehat{NAM}=90^0\)(\(\widehat{BAC}=90^0\), M∈AB, N∈AC)
\(\widehat{AMH}=90^0\)(HM⊥AB)
\(\widehat{ANH}=90^0\)(HN⊥AC)
Do đó: AMHN là hình chữ nhật(Dấu hiệu nhận biết hình chữ nhật)
b) Ta có: ΔABC vuông tại A(gt)
nên \(S_{ABC}=\dfrac{AB\cdot AC}{2}=\dfrac{6\cdot8}{2}=24\left(cm^2\right)\)(1)
Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=6^2+8^2=100\)
hay BC=10(cm)
Xét ΔABC có AH là đường cao ứng với cạnh BC(gt)
nên \(S_{ABC}=\dfrac{AH\cdot BC}{2}=AH\cdot\dfrac{10}{2}=5\cdot AH\)(2)
Từ (1) và (2) suy ra \(5\cdot AH=24\)
hay AH=4,8cm
Ta có: AMHN là hình chữ nhật(cmt)
nên AH=MN(Hai đường chéo trong hình chữ nhật AMHN)
mà AH=4,8cm(cmt)
nên MN=4,8cm
Vậy: MN=4,8cm
C
15 tháng 8 2023
Xét tứ giác AEHD, có:
∠A = ∠E = ∠D = 90°
=> tứ giác AEHD là hình chữ nhật.
O là giao điểm hai đường chéo hcn AEHD
=> OD = OH (1).
DI là đường trung tuyến ứng với cạnh huyền của Δ vuông DHB
=> DI = 1/2 BH = IH (2).
Xét Δ IDO và Δ IHO, có:
OD = OH (1).
OI là cạnh chung.
DI = IH (2).
=> Δ IDO = Δ IHO (đpcm).
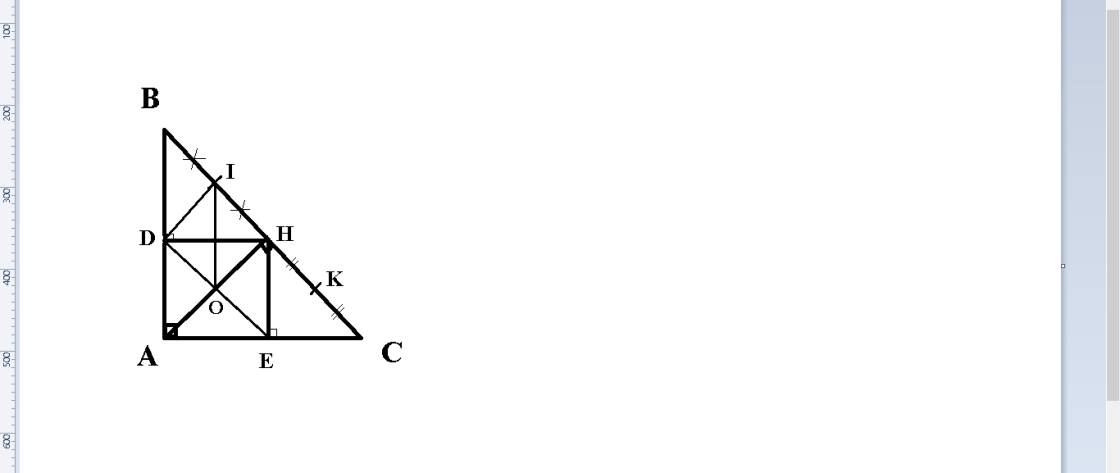
(bồ xem thử ổn hông nhe).
a: \(BC=\sqrt{3^2+4^2}=5\left(cm\right)\)
XétΔABC vuông tại A có \(\sin C=\dfrac{AB}{BC}=\dfrac{3}{5}\)
nên \(\widehat{C}\simeq37^0\)
=>\(\widehat{B}\simeq53^0\)
b: \(AH=\dfrac{AB\cdot AC}{BC}=2.4\left(cm\right)\)
\(HB=\dfrac{BA^2}{BC}=\dfrac{3^2}{5}=1.8\left(cm\right)\)
HC=BC-HB=3,2(cm)
c: Xét ΔAHB vuông tại H có HM là đường cao
nên \(AM\cdot AB=AH^2\left(1\right)\)
Xét ΔHCA vuông tại H có HN là đường cao
nên \(AN\cdot AC=AH^2\left(2\right)\)
Từ (1) và (2) suy ra \(AM\cdot AB=AN\cdot AC\)
d: Xét tứgiác AMHN có \(\widehat{AMH}+\widehat{ANH}=180^0\)
nên AMHN là tứ giác nội tiếp
Xét (AH/2) có
\(\widehat{ANM}\) là góc nội tiếp chắn cung AM
\(\widehat{AHM}\) là góc nội tiếp chắn cung AM
DO đó: \(\widehat{ANM}=\widehat{AHM}=\widehat{B}\)
Ta có: ΔABC vuông tại A
mà AE là đường trung tuyến
nên AE=CE
=>\(\widehat{EAC}=\widehat{C}\)
\(\widehat{ANM}+\widehat{EAC}=\widehat{B}+\widehat{C}=90^0\)
=>AE\(\perp\)MN