trong mặt phẳng tọa độ Oxy ,cho 3 điểm A(5;2),B(5;-2), C(4;-3) . Đường thẳng đi qua điểm A và vuông góc với đường thẳng BC có phương trình là
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PN
1
NV
Nguyễn Việt Lâm
Giáo viên
3 tháng 10 2019
Áp dụng công thức tọa độ trung điểm:
\(\left\{{}\begin{matrix}x_I=\frac{x_A+x_B}{2}=2\\y_I=\frac{y_A+y_B}{2}=1\end{matrix}\right.\)
\(\Rightarrow I\left(2;1\right)\)
YY
3
HP
12 tháng 2 2016
bn vẽ hình ra là sẽ thấy BAC là góc vuông =>BAC=900,mk lười vẽ quá
AH
Akai Haruma
Giáo viên
17 tháng 12 2021
Lời giải:
$\overrightarrow{MN}-\overrightarrow{MP}=\overrightarrow{PN}=(x_N-x_P, y_N-y_P)=(4, -3)$
CM
19 tháng 1 2017
Gọi D(x; y)
Ta có A D → = x + 2 ; y và B C → = 4 ; − 3 .
Vì ABCD là hình bình hành nên A D → = B C →
x + 2 = 4 y = − 3 ⇔ x = 2 y = − 3 ⇒ D 2 ; − 3 .
Chọn A.
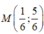
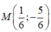
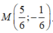
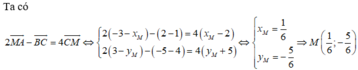
A(5;2); B(5;-2); C(4;-3)
Gọi (d): ax+by+c=0 là phương trình đường thẳng cần tìm
Vì (d)\(\perp\)BC nên (d) nhận vecto BC làm vecto pháp tuyến
\(\overrightarrow{BC}=\left(-1;-1\right)=\left(1;1\right)\)
=>(d) nhận \(\overrightarrow{BC}=\left(1;1\right)\) làm vecto pháp tuyến
mà (d) đi qua A(5;2)
nên phương trình đường thẳng (d) là:
1(x-5)+1(y-2)=0
=>x-5+y-2=0
=>x+y-7=0