\(6\sqrt{2x+7}=2\sqrt{x}+x+15\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(6\sqrt{2x+7}=2\sqrt{x}+x+15\left(1\right)\)
\(Đk:x\ge0\)
\(\left(1\right)\Leftrightarrow x+2\sqrt{x}+15-6\sqrt{2x+7}=0\)
\(\Leftrightarrow\left[\left(2x+7\right)-6\sqrt{2x+7}+9\right]-\left(x-2\sqrt{x}+1\right)=0\)
\(\Leftrightarrow\left(\sqrt{2x+7}-3\right)^2-\left(\sqrt{x}-1\right)^2=0\)
\(\Leftrightarrow\left(\sqrt{2x+7}+\sqrt{x}-4\right)\left(\sqrt{2x+7}-\sqrt{x}-2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}\sqrt{2x+7}+\sqrt{x}=4\left(2\right)\\\sqrt{2x+7}-\sqrt{x}=2\left(3\right)\end{matrix}\right.\)
\(\left(2\right)\Leftrightarrow\left(2x+7\right)+2\sqrt{x\left(2x+7\right)}+x=16\)
\(\Leftrightarrow2\sqrt{x\left(2x+7\right)}=9-3x\)
\(\Leftrightarrow\left\{{}\begin{matrix}9-3x\ge0\\4x\left(2x+7\right)=81-54x+9x^2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\le3\\x^2-82x+81=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\le3\\\left[{}\begin{matrix}x=1\left(n\right)\\x=81\left(l\right)\end{matrix}\right.\end{matrix}\right.\) \(\Leftrightarrow x=1\left(n\right)\)
\(\left(3\right)\Leftrightarrow\left(2x+7\right)-2\sqrt{x\left(2x+7\right)}+x=4\) (vì \(\sqrt{2x+7}>\sqrt{x}\))
\(\Leftrightarrow2\sqrt{x\left(2x+7\right)}=3x+3\)
\(\Leftrightarrow\left\{{}\begin{matrix}3x+3\ge0\\4x\left(2x+7\right)=9x^2+18x+9\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge-1\\x^2-10x+9=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge-1\\\left[{}\begin{matrix}x=1\left(n\right)\\x=9\left(n\right)\end{matrix}\right.\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=9\end{matrix}\right.\left(n\right)\)
Vậy phương trình (1) có 2 nghiệm là \(x=1\text{v}ax=9\)
bạn ơi sao từ đoạn trên lại ra được tích như dưới vậy ạ
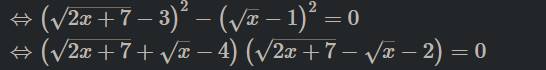

do \(x^2+x+1=x^2+2.\frac{1}{2}x+\frac{1}{4}+\frac{3}{4}=\left(x+\frac{1}{2}\right)^2+\frac{3}{4}>0\forall x\)
\(\Rightarrow\sqrt{x^2+x+1}>0\forall x\)
voi dk \(x\ge-1\) ta co
\(x^2+x+1=x^2+2x+1\Rightarrow x=0\)(tm)
b,\(\sqrt{4x^2-20x+25}+2x=5\)
\(\Leftrightarrow\sqrt{\left(2x-5\right)^2}+2x=5\)
\(\Leftrightarrow\left|2x-5\right|+2x=5\)
th1 \(2x-5\ge0\Leftrightarrow x\ge\frac{5}{2}\) ta co\(2x-5+2x=5\Leftrightarrow4x=10\Rightarrow x=2.5\left(tm\right)\)
th2 \(2x-5< 0\Leftrightarrow x< \frac{5}{2}\) \(5-2x+2x=5\Leftrightarrow5=5\)
\(\Rightarrow\) dung voi moi \(x< \frac{5}{2}\)
kl \(x\le\frac{5}{2}\)
c, \(\left|x-1\right|=4\) \(\Rightarrow\orbr{\begin{cases}x-1=4\left(x\ge1\right)\\x-1=-4\left(x< 1\right)\end{cases}\Leftrightarrow\orbr{\begin{cases}x=5\left(tm\right)\\x=-3\left(tm\right)\end{cases}}}\)
d.\(\sqrt{3\left(x^2+2x+1\right)+4}+\sqrt{5\left(x^2+2x+1\right)+16}\)
=\(\sqrt{3\left(x+1\right)^2+4}+\sqrt{5\left(x+1\right)^2+16}\ge\sqrt{4}+\sqrt{16}=6\)
ma \(-x^2-2x+5=-\left(x^2+2x+1\right)+6=-\left(x+1\right)^2+6\le6\)
dau = xay ra \(\Leftrightarrow x=-1\)

c.
ĐKXĐ: \(\left[{}\begin{matrix}x\le-5\\x\ge6\end{matrix}\right.\)
\(\sqrt{\left(x-3\right)\left(x-5\right)}+\sqrt{\left(x-3\right)\left(x+5\right)}=\sqrt{\left(x-3\right)\left(x-6\right)}\)
- Với \(x\ge6\) , do \(x-3>0\) pt trở thành:
\(\sqrt{x-5}+\sqrt{x+5}=\sqrt{x-6}\)
Do \(\left\{{}\begin{matrix}\sqrt{x-5}>\sqrt{x-6}\\\sqrt{x+5}>0\end{matrix}\right.\) \(\Rightarrow\sqrt{x-5}+\sqrt{x+5}>\sqrt{x-6}\) pt vô nghiệm
- Với \(x\le-5\) pt tương đương:
\(\sqrt{\left(3-x\right)\left(5-x\right)}+\sqrt{\left(3-x\right)\left(-x-5\right)}=\sqrt{\left(3-x\right)\left(6-x\right)}\)
Do \(3-x>0\) pt trở thành:
\(\sqrt{5-x}+\sqrt{-x-5}=\sqrt{6-x}\)
\(\Leftrightarrow-2x+2\sqrt{x^2-25}=6-x\)
\(\Leftrightarrow2\sqrt{x^2-25}=x+6\) (\(x\ge-6\))
\(\Leftrightarrow4\left(x^2-25\right)=x^2+12x+36\)
\(\Leftrightarrow3x^2-12x-136=0\Rightarrow x=\dfrac{6-2\sqrt{111}}{3}\)
a.
Kiểm tra lại đề, pt này không giải được
b.
ĐKXĐ: \(x\ge0\)
\(\sqrt{x\left(x+1\right)}-\sqrt{x}+1-\sqrt{x+1}=0\)
\(\Leftrightarrow\sqrt{x}\left(\sqrt{x+1}-1\right)-\left(\sqrt{x+1}-1\right)=0\)
\(\Leftrightarrow\left(\sqrt{x}-1\right)\left(\sqrt{x+1}-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}\sqrt{x}=1\\\sqrt{x+1}=1\end{matrix}\right.\)
\(\Leftrightarrow...\)

Lời giải:
a. ĐKXĐ: $x\geq -9$
PT $\Leftrightarrow x+9=7^2=49$
$\Leftrightarrow x=40$ (tm)
b. ĐKXĐ: $x\geq \frac{-3}{2}$
PT $\Leftrightarrow 4\sqrt{2x+3}-\sqrt{4(2x+3)}+\frac{1}{3}\sqrt{9(2x+3)}=15$
$\Leftrightarrow 4\sqrt{2x+3}-2\sqrt{2x+3}+\sqrt{2x+3}=15$
$\Leftrgihtarrow 3\sqrt{2x+3}=15$
$\Leftrightarrow \sqrt{2x+3}=5$
$\Leftrightarrow 2x+3=25$
$\Leftrightarrow x=11$ (tm)
c.
PT \(\Leftrightarrow \left\{\begin{matrix} 2x+1\geq 0\\ x^2-6x+9=(2x+1)^2\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x\geq \frac{-1}{2}\\ 3x^2+10x-8=0\end{matrix}\right.\)
\(\Leftrightarrow \left\{\begin{matrix} x\geq \frac{-1}{2}\\ (3x-2)(x+4)=0\end{matrix}\right.\)
\(\Leftrightarrow x=\frac{2}{3}\)
d. ĐKXĐ: $x\geq 1$
PT \(\Leftrightarrow \sqrt{(x-1)+4\sqrt{x-1}+4}-\sqrt{(x-1)+6\sqrt{x-1}+9}=9\)
\(\Leftrightarrow \sqrt{(\sqrt{x-1}+2)^2}-\sqrt{(\sqrt{x-1}+3)^2}=9\)
\(\Leftrightarrow \sqrt{x-1}+2-(\sqrt{x-1}+3)=9\)
\(\Leftrightarrow -1=9\) (vô lý)
Vậy pt vô nghiệm.

mầy câu 1;3;;4;5 cách làm nhu nhau(nhân liên hop hoac bình phuong lên)
1.
\(DK:x\in\left[-4;5\right]\)
\(\Leftrightarrow\sqrt{x-5}+\left(\sqrt{x+4}-3\right)=0\)
\(\Leftrightarrow\sqrt{x-5}+\frac{x-5}{\sqrt{x+4}+3}=0\)
\(\Leftrightarrow\sqrt{x-5}\left(1+\frac{\sqrt{x-5}}{\sqrt{x+4}+3}\right)=0\)
Vi \(1+\frac{\sqrt{x-5}}{\sqrt{x+4}+3}>0\)
\(\Rightarrow\sqrt{x-5}=0\)
\(x=5\left(n\right)\)
Vay nghiem cua PT la \(x=5\)
2.
\(DK:x\ge0\)
\(\Leftrightarrow\sqrt{\left(\sqrt{x}-2\right)^2}+\sqrt{\left(\sqrt{x}-3\right)^2}=1\)
\(\Leftrightarrow|\sqrt{x}-2|+|\sqrt{x}-3|=1\)
Ta co:
\(|\sqrt{x}-2|+|\sqrt{x}-3|=|\sqrt{x}-2|+|3-\sqrt{x}|\ge|\sqrt{x}-2+3-\sqrt{x}|=1\)
Dau '=' xay ra khi \(\left(\sqrt{x}-2\right)\left(3-\sqrt{x}\right)\ge0\)
TH1:
\(\hept{\begin{cases}\sqrt{x}-2\ge0\\3-\sqrt{x}\ge0\end{cases}\Leftrightarrow4\le x\le9\left(n\right)}\)
TH2:(loai)
Vay nghiem cua PT la \(x\in\left[4;9\right]\)

8) ĐKXĐ: $-2\leq x\leq 1$
PT $\Leftrightarrow (2x+4)-4\sqrt{2x+4}+4+[(1-x)-2\sqrt{1-x}+1]=0$
$\Leftrightarrow (\sqrt{2x+4}-2)^2+(\sqrt{1-x}-1)^2=0$
Dễ thấy: $(\sqrt{2x+4}-2)^2; (\sqrt{1-x}-1)^2\geq 0$ với mọi $x\in [-2;1]$ nên để tổng của chúng bằng $0$ thì:
$(\sqrt{2x+4}-2)^2=(\sqrt{1-x}-1)^2=0$
$\Leftrightarrow \sqrt{2x+4}=2; \sqrt{1-x}-1=0$
$\Leftrightarrow x=0$ (thỏa mãn)
Vậy.....
7)
ĐKXĐ: $x\geq -1$
PT $\Leftrightarrow x^2+[(x+1)-2\sqrt{x+1}+1]=0$
$\Leftrightarrow x^2+(\sqrt{x+1}-1)^2=0$
Ta thấy:
$x^2\geq 0; (\sqrt{x+1}-1)^2\geq 0$ với mọi $x\geq -1$
Do đó để tổng của chúng bằng $0$ thì $x^2=(\sqrt{x+1}-1)^2=0$
$\Leftrightarrow x=0$ (thỏa mãn)
Vậy.......

a.
\(A=\frac{1}{\sqrt{1}+\sqrt{3}}+\frac{1}{\sqrt{3}+\sqrt{5}}+\frac{1}{\sqrt{5}+\sqrt{7}}+\frac{1}{\sqrt{7}+\sqrt{9}}\)
\(=\frac{\sqrt{3}-\sqrt{1}}{3-1}+\frac{\sqrt{5}-\sqrt{3}}{5-3}+\frac{\sqrt{7}-\sqrt{5}}{7-5}+\frac{\sqrt{9}-\sqrt{7}}{9-7}\)
\(=\frac{\sqrt{9}-\sqrt{7}+\sqrt{7}-\sqrt{5}+\sqrt{5}-\sqrt{3}+\sqrt{3}-\sqrt{1}}{2}\)
\(=\frac{3-1}{2}=1\)
b.
\(B=2\sqrt{40\sqrt{12}}-2\sqrt{\sqrt{75}}-3\sqrt{5\sqrt{48}}\)
\(=2\sqrt{80\sqrt{3}}-2\sqrt{5\sqrt{3}}-3\sqrt{20\sqrt{3}}\)
\(=8\sqrt{5\sqrt{3}}-2\sqrt{5\sqrt{3}}-6\sqrt{5\sqrt{3}}=0\)
c.
\(C=\frac{15}{\sqrt{6}+1}+\frac{4}{\sqrt{6}-2}-\frac{12}{3-\sqrt{6}}-\sqrt{6}\)
\(=\frac{15\sqrt{6}-15}{6-1}+\frac{4\sqrt{6}+8}{6-4}-\frac{36+12\sqrt{6}}{9-6}-\sqrt{6}\)
\(=\frac{15\sqrt{6}-15}{5}+\frac{4\sqrt{6}+8}{2}-\frac{36+12\sqrt{6}}{3}-\sqrt{6}\)
\(=3\sqrt{6}-3+2\sqrt{6}+4-12-4\sqrt{6}-\sqrt{6}\)
\(=-11\)
d)D=\(\sqrt{x+2\sqrt{2x-4}}+\sqrt{x-2\sqrt{2x-4}}\)( \(x\ge2\))
=\(\sqrt{x+2\sqrt{2}.\sqrt{x-2}}+\sqrt{x-2\sqrt{2}.\sqrt{x-2}}\)
=\(\sqrt{\left(x-2\right)+2\sqrt{2}.\sqrt{x-2}+2}+\sqrt{\left(x-2\right)-2\sqrt{2}.\sqrt{x-2}+2}\)
=\(\sqrt{\left(\sqrt{x-2}+\sqrt{2}\right)^2}+\sqrt{\left(\sqrt{x-2}-\sqrt{2}\right)^2}\)
=\(\sqrt{x-2}+\sqrt{2}+\left|\sqrt{x-2}-\sqrt{2}\right|\)(1)
TH1: \(2\le x\le4\)
Từ (1)<=> \(\sqrt{x-2}+\sqrt{2}-\sqrt{x-2}+\sqrt{2}\)
=\(2\sqrt{2}\)
TH2. x\(>4\)
Từ (1) <=> \(\sqrt{x-2}+\sqrt{2}-\sqrt{2}+\sqrt{x-2}\)=\(2\sqrt{x-2}\)
Vậy \(\left[{}\begin{matrix}2\le x\le4\\x>4\end{matrix}\right.< =>\left[{}\begin{matrix}D=2\sqrt{2}\\D=2\sqrt{x-2}\end{matrix}\right.\)
Đk: \(x\ge0\)
pt đã cho \(\Leftrightarrow6\sqrt{2x+7}-\left(\dfrac{3}{2}x+\dfrac{33}{2}\right)=2\sqrt{x}-\left(\dfrac{1}{2}x+\dfrac{3}{2}\right)\)
\(\Leftrightarrow\dfrac{36\left(2x+7\right)-\left(\dfrac{3}{2}x+\dfrac{33}{2}\right)^2}{6\sqrt{2x+7}+\dfrac{3}{2}x+\dfrac{33}{2}}=\dfrac{4x-\left(\dfrac{1}{2}x+\dfrac{3}{2}\right)^2}{2\sqrt{x}+\dfrac{1}{2}x+\dfrac{3}{2}}\)
\(\Leftrightarrow\dfrac{72x+252-\dfrac{9}{4}x^2-\dfrac{99}{2}x-\dfrac{1089}{4}}{6\sqrt{2x+7}+\dfrac{3}{2}x+\dfrac{33}{2}}=\dfrac{4x-\dfrac{1}{4}x^2-\dfrac{3}{2}x-\dfrac{9}{4}}{2\sqrt{x}+\dfrac{1}{2}x+\dfrac{3}{2}}\)
\(\Leftrightarrow\dfrac{-\dfrac{9}{4}x^2+\dfrac{45}{2}x-\dfrac{81}{4}}{6\sqrt{2x+7}+\dfrac{3}{2}x+\dfrac{33}{2}}=\dfrac{-\dfrac{1}{4}x^2+\dfrac{5}{2}x-\dfrac{9}{4}}{2\sqrt{x}+\dfrac{1}{2}x+\dfrac{3}{2}}\)
\(\Leftrightarrow\dfrac{x^2-10x+9}{-\dfrac{4}{9}\left(6\sqrt{2x+7}+\dfrac{3}{2}x+\dfrac{33}{2}\right)}=\dfrac{x^2-10x+9}{-4\left(2\sqrt{x}+\dfrac{1}{2}x+\dfrac{3}{2}\right)}\)
\(\Leftrightarrow\left(x^2-10x+9\right)\left[\dfrac{9}{4\left(6+\sqrt{2x+7}+\dfrac{3}{2}x+\dfrac{33}{2}\right)}-\dfrac{1}{4\left(2\sqrt{x}+\dfrac{1}{2}x+\dfrac{3}{2}\right)}\right]=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x^2-10x+9=0\\\dfrac{9}{6\sqrt{2x+7}+\dfrac{3}{2}x+\dfrac{33}{2}}=\dfrac{1}{2\sqrt{x}+\dfrac{1}{2}x+\dfrac{3}{2}}\end{matrix}\right.\)
Với \(x^2-10x+9=0\Leftrightarrow\left(x-1\right)\left(x-9\right)=0\) \(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=9\end{matrix}\right.\) (nhận)
pt nhỏ thứ 2 \(\Leftrightarrow18\sqrt{x}+\dfrac{9}{2}x+\dfrac{27}{2}=6\sqrt{2x+7}+\dfrac{3}{2}x+\dfrac{33}{2}\)
\(\Leftrightarrow6\sqrt{2x+7}-18\sqrt{x}=3x-3\)
\(\Leftrightarrow2\sqrt{2x+7}-6\sqrt{x}=x-1\)
\(\Leftrightarrow\dfrac{4\left(2x+7\right)-36x}{2\sqrt{2x+7}+6\sqrt{x}}=x-1\)
\(\Leftrightarrow\dfrac{28-28x}{2\sqrt{2x+7}+6\sqrt{x}}=x-1\)
\(\Leftrightarrow\left(x-1\right)\left(1+\dfrac{28}{2\sqrt{2x+7}+6\sqrt{x}}\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\left(nhận\right)\\1+\dfrac{28}{2\sqrt{2x+7}+6\sqrt{x}}=0\left(loại\right)\end{matrix}\right.\)
Vậy pt đã cho có tập nghiệm \(S=\left\{1;9\right\}\)