tam giác ABC vuông tại A ,AB =AC =a
(O ; \(\frac{AC}{2}\)) cắt BC tại O
a) CM: tam giác ABC vuông cân
I là trung điểm CB .Cm : CI x CB =\(\frac{a^2}{2}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

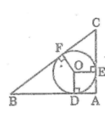
Áp dụng định lí Pitago vào tam giác vuông ABC ta có :
B C 2 = A B 2 + A C 2 = 3 2 + 4 2 = 25
Suy ra : BC = 5 (cm)
Theo tính chất hai tiếp tuyến giao nhau ta có:
AD = AE
BD = BF
CE = CF
Mà: AD = AB – BD
AE = AC – CF
Suy ra: AD + AE = AB – BD + (AC – CF)
= AB + AC – (BD + CF)
= AB + AC – (BF + CF)
= AB + AC – BC
Suy ra:
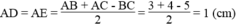

a, Kẻ OH vuông góc với BC
Ta có tam giác BEO=BHO( ch-gn )
=> BE=BH
Tương tự ta có : CH=CF
Mà BH+HC=BC => BE+CF=BC=5 ( Bạn tính BC theo định lý Pytago tam giác ABC nk )
Mà AB+AC=BE+FC+AE+AF=7 ( AE=AF vì AEOF là hình vuông )
=> AE=(7-5):2=1
=> AB+AC-BC=3+4-5=2=2AE ( đpcm )

1
\(\dfrac{AB}{AC}=\dfrac{3}{4}\Rightarrow AB=\dfrac{3}{.4}AC\)
Theo pytago xét tam giác ABC vuông tại A có:
\(\sqrt{AB^2+AC^2}=BC^2\\ \Rightarrow\sqrt{\left(\dfrac{3}{4}AC\right)^2+AC^2}=10\\ \Rightarrow AC=8\\ \Rightarrow AB=\dfrac{3.8}{4}=6\)
Theo hệ thức lượng xét tam giác ABC vuông tại A, đường cao AH có:
\(AB^2=BH.BC\\ \Leftrightarrow BH=\dfrac{AH^2}{BC}=\dfrac{6^2}{10}=3,6\)
2
\(\dfrac{AB}{AC}=\dfrac{27}{4}\Rightarrow AB=\dfrac{27}{4}AC\)
\(BC=\sqrt{AB^2+AC^2}=\sqrt{\left(\dfrac{27}{4}AC\right)^2+AC^2}=\dfrac{\sqrt{745}AC}{4}\) ( Theo pytago trong tam giác ABC vuông tại A)
Theo hệ thức lượng trong tam giác ABC vuông tại A, đường cao AH có:
\(AH.BC=AB.AC\\ \Leftrightarrow33,6.\dfrac{\sqrt{745}}{4}AC=\dfrac{27}{4}AC.AC\\ \Rightarrow AC=\dfrac{56\sqrt{745}}{45}\)
\(\Rightarrow\left\{{}\begin{matrix}AB=\dfrac{27}{4}.\dfrac{56\sqrt{745}}{45}=\dfrac{42\sqrt{745}}{5}\\BC=\dfrac{\sqrt{745}}{4}.\dfrac{56\sqrt{745}}{45}=\dfrac{2086}{9}\end{matrix}\right.\)
Vậy \(\left\{{}\begin{matrix}AC\approx33,97\\AB\approx229,28\\BC\approx231,78\end{matrix}\right.\)
3
`BC=HB+HC=36+64=100`
Theo hệ thức lượng có (trong tam giác ABC vuông tại A đường cao AH):
\(AH^2=HB.HC\\ \Rightarrow AH=\sqrt{36.64}=48\)
\(AB=\sqrt{HB.BC}=\sqrt{36.100}=60\\ AC=\sqrt{HC.BC}=\sqrt{64.100}=80\)

a: Xét (O) có
ΔAHB nội tiếp
AB là đường kính
=>ΔAHB vuông tại H
=>AH vuông góc BC
b: ΔHAC vuông tại H nên ΔAHC nội tiếp đường tròn đường kính AC
=>KA=KH=KC
Xét ΔKAO và ΔKHO có
KA=KH
AO=HO
KO chung
=>ΔKAO=ΔKHO
=>góc KHO=góc KAO=90 độ
MK KO HIỂU LẮM