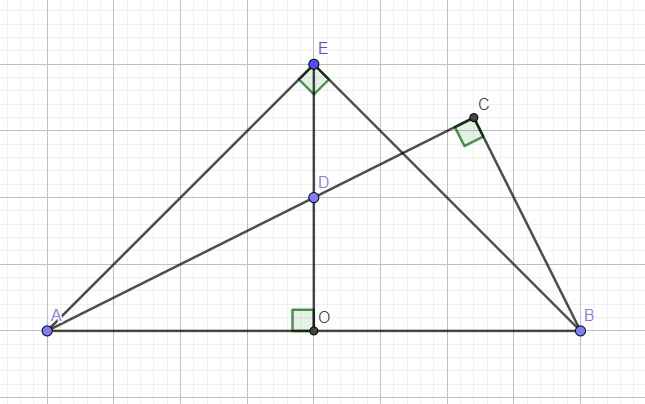
Cho đoạn thẳng AB=2a.Từ trung điểm O của AB kẻ Ox vuông góc với AB tại O.Trên Ox lấy D sao cho OD = a:2.Kẻ BC vuông góc với BC tại C(AD kéo dài)
a/tính AD,AC,BC theo a
b/Kéo dài DO 1 đoạn DE bằng a.CM A,B.C cùng nằm trên 1 đường tròn
c/vẽ đường vuông góc vs BC tai B cắt CE tại F.Tính BF
d/Gọi P là giao điểm của AF và CE.tính AF và BF
thanks ..

a) x4+x3+2x2+x+1=(x4+x3+x2)+(x2+x+1)=x2(x2+x+1)+(x2+x+1)=(x2+x+1)(x2+1)
b)a3+b3+c3-3abc=a3+3ab(a+b)+b3+c3 -(3ab(a+b)+3abc)=(a+b)3+c3-3ab(a+b+c)
=(a+b+c)((a+b)2-(a+b)c+c2)-3ab(a+b+c)=(a+b+c)(a2+2ab+b2-ac-ab+c2-3ab)=(a+b+c)(a2+b2+c2-ab-ac-bc)
c)Đặt x-y=a;y-z=b;z-x=c
a+b+c=x-y-z+z-x=o
đưa về như bài b
d)nhóm 2 hạng tử đầu lại và 2hangj tử sau lại để 2 hạng tử sau ở trong ngoặc sau đó áp dụng hằng đẳng thức dề tính sau đó dặt nhân tử chung
e)x2(y-z)+y2(z-x)+z2(x-y)=x2(y-z)-y2((y-z)+(x-y))+z2(x-y)
=x2(y-z)-y2(y-z)-y2(x-y)+z2(x-y)=(y-z)(x2-y2)-(x-y)(y2-z2)=(y-z)(x2-2y2+xy+xz+yz)
tui cũng ko biết làm ai làm giúp với