CHO TỨ GIÁC ABCD, GỌI M, N LẦN LƯỢT LÀ TRUNG ĐIỂM AB, CD CHỨNG MINH RẰNG:
BC + AD = 2MN = AC + BD ( trên đầu đều có vecto)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
5 tháng 12 2017
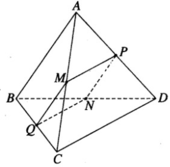
Ta có MPNQ là hình bình hành vì
Do đó
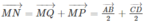
hay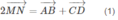 
Mặt khác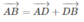 
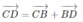
Nên
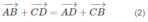
Vì
Từ (1) và (2) ta có:
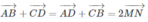
là đẳng thức cần chứng minh
6 tháng 10 2018
Sử dụng đường trung bình, ta có: KN = 1/2 AB, NI = 1/2 CD , IM = 1/2 AB , MK = 1/2 CD
Mà AB = CD (gt)
\(\Rightarrow KN=NI=IM=MK\)
\(\Rightarrow KNIM\)là hình thoi
Do đó: MN là tia phân giác của \(\widehat{IMK}\)(tính chất hình thoi)
Chúc bạn học tốt.
27 tháng 10 2021
Xét ΔABC có
E là trung điểm của AB
N là trung điểm của AC
Do đó: EN là đường trung bình của ΔABC
Suy ra: EN//BC và \(EN=\dfrac{BC}{2}\left(1\right)\)
Xét ΔBDC có
M là trung điểm của BD
F là trung điểm của CD
Do đó: MF là đường trung bình của ΔBDC
Suy ra: MF//BC và \(MF=\dfrac{BC}{2}\left(2\right)\)
Xét ΔABD có
E là trung điểm của AB
M là trung điểm của BD
Do đó: EM là đường trung bình của ΔABD
Suy ra: \(EM=\dfrac{AD}{2}=\dfrac{BC}{2}\left(3\right)\)
Từ (1) và (2) suy ra EN//MF và EN=MF
Từ (1) và (3) suy ra EN=EM
Xét tứ giác ENFM có
EN//MF
EN=MF
Do đó: ENFM là hình bình hành
mà EN=EM
nên ENFM là hình thoi
CM
4 tháng 6 2019
Ta có:
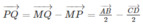
Do đó:
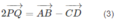
Mặt khác:
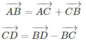
Nên
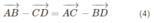
Vì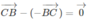 
Từ (3) và (4) ta suy ra
là đẳng thức cần chứng minh.
16 tháng 8 2022
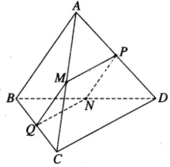
Xét ΔBAD có
M,Q lần lượt là tđiểm của AB và AD
nên MQ là đường trung bình
=>MQ//BD và MQ=BD/2(1)
Xét ΔBCD có
N,P lần lượt là trung điểm của CB và CD
nên NP là đường trung bình
=>NP//BD và NP=BD/2(2)
Từ (1) và (2) suy ra MNPQ là hình bình hành(5)
Xét ΔABC có
M,N lần lượt là trung điểm của BA và BC
nên MN là đường trung bình
=>MN=AC/2=BD/2=MQ(3) và MN//AC
=>MN vuông góc với MQ(4)
Từ (3), (4)và (5) suy ra MNPQ là hình vuông
Ta có \(2\overrightarrow{MN}=\overrightarrow{MD}+\overrightarrow{MC}=\overrightarrow{MA}+\overrightarrow{AD}+\overrightarrow{MB}+\overrightarrow{BC}=\overrightarrow{AD}+\overrightarrow{BC}\)
( do vecto MA + vecto MB = 0 )
Lại có \(2\overrightarrow{NM}=\overrightarrow{NA}+\overrightarrow{NB}=\overrightarrow{NC}+\overrightarrow{CA}+\overrightarrow{ND}+\overrightarrow{DB}=\overrightarrow{CA}+\overrightarrow{DB}\)
( do vecto NC + vecto ND = 0 )
\(\Leftrightarrow2\overrightarrow{MN}=\overrightarrow{AC}+\overrightarrow{BD}\)