a) Tính AH
b) Tính góc nhị diện [A, A'B',C']
c) Tính góc nhị diện [B,B'C',A']
d) Tính thể tích của lăng trụ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
Dễ dàng tính được các cạnh của tứ diện CA′B′C′:
A ' C = A ' C ' = CC ' = B ' C ' = A ' B ' = a .
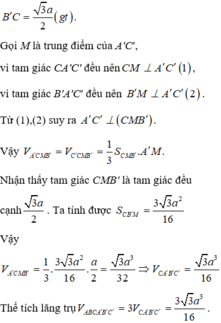
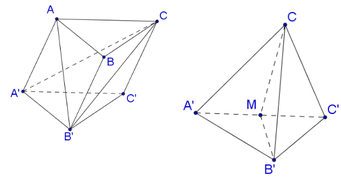

Lời giải:
Từ $A$ kẻ $AH$ vuông góc với $BC$
Khi đó:
\(60^0=\angle ((A'BC), (ABC))=\angle (AH, A'H)=\angle AHA'\)
Do hình lăng trụ đã cho là lăng trụ đều nên tam giác $ABC$ là tam giác đều có đường cao $AH$ nên:
\(AH=\sqrt{a^2-(\frac{a}{2})^2}=\frac{\sqrt{3}a}{2}\)
\(\Rightarrow \sqrt{3}=\tan AHA'=\frac{AA'}{AH}\Rightarrow AA'=\frac{3}{2}a\)
\(V_{ABC.A'B'C'}=S_{ABC}.AA'=\frac{AH.BC}{2}.\frac{3}{2}a=\frac{\sqrt{3}a^2}{4}.\frac{3}{2}a=\frac{3\sqrt{3}a^3}{8}\)

bạn xem lại đề bài đi, vì A'B' // (ABC) mà sao tạo góc 60 đc

Lời giải:
Áp dụng định lý Pitago:
$BC=\sqrt{AB^2+AC^2}=\sqrt{9^2+12^2}=15$ (cm)
$CC'=\sqrt{BC'^2-BC^2}=\sqrt{17^2-15^2}=8$ (cm)
Diện tích xung quanh hình lăng trụ là:
$(9+12+15).8=288$ (cm2)

Gọi thể tích lăng trụ là V, gọi M là trung điểm B'C'
\(\Rightarrow V_{ABF.A'B'M}=\frac{1}{2}V\)
\(V_{B'.AA'MF}=\frac{2}{3}V_{ABF.A'B'M}=\frac{1}{3}V\)
\(S_{AEF}=\frac{1}{2}S_{AA'MF}\Rightarrow V_{B'.AEF}=\frac{1}{2}V_{B'.AA'MF}=\frac{1}{6}V\)

a. Do \(AC||A'C'\Rightarrow\) giao tuyến của (AB'C) và (A'B'C') là đường thẳng qua B' và song song A'C'
Qua B kẻ \(d||A'C'\Rightarrow d=\left(AB'C\right)\cap\left(A'B'C'\right)\)
b. Trong mp (ABB'A'), gọi M là giao điểm AB' và A'B
Trong mp (BCC'B'), gọi N là giao điểm BC' và B'C
\(\Rightarrow MN=\left(AB'C\right)\cap\left(A'BC'\right)\)
Mặt khác do các mặt bên của lăng trụ là các hình bình hành
\(\Rightarrow\) M là trung điểm AB' và A'B, N là trung điểm BC' và B'C
\(\Rightarrow MN||AC\) (đường trung bình)
\(\Rightarrow\left\{{}\begin{matrix}MN||\left(ABC\right)\\MN||\left(AA'C'C\right)\end{matrix}\right.\)
MN song song (A'B'C) là sai, MN chỉ song song (A'B'C')

Bạn tự vẽ hình, lăng trụ khá xấu nên làm biếng vẽ quá, mà đề bài yêu cầu tính gì nhỉ? Diện tích mặt cầu ngoại tiếp lăng trụ?
Kẻ \(AH\perp BC\Rightarrow AH\perp\left(BCC'B'\right)\Rightarrow\widehat{AC'H}\) là góc giữa AC' và (BCC'B')
\(AC=\sqrt{BC^2-AB^2}=a\Rightarrow AH=\frac{AB.AC}{BC}=\frac{a\sqrt{3}}{2}\)
\(AC'=\frac{AH}{sin\widehat{AC'H}}=\frac{AH}{sin30^0}=a\sqrt{3}\Rightarrow CC'=\sqrt{AC'^2-AC^2}=a\sqrt{2}\)
Gọi M là trung điểm BC, N là trung điểm B'C', I là trung điểm MN \(\Rightarrow I\) là tâm mặt cầu ngoại tiếp lăng trụ đồng thời là tâm hcn BCC'B'
\(R=IB=\frac{1}{2}BC'=\frac{1}{2}\sqrt{BC^2+CC'^2}=\frac{a\sqrt{6}}{2}\)
\(\Rightarrow S=4\pi R^2=6\pi a^2\)
a) Có \(A'H=\dfrac{a\sqrt{3}}{2}\). Lại có \(AH\perp\left(A'B'C'\right)\) tại H nên \(\widehat{AA',\left(A'B'C'\right)}=\widehat{AA'H}=60^o\)
\(\Rightarrow AH=A'H.\tan60^o\) \(=\dfrac{a\sqrt{3}}{2}.\sqrt{3}=\dfrac{3a}{2}\)
b) Kẻ \(HK\perp A'B'\) tại K, \(HL\perp AK\) tại L.
Ta thấy \(A'B'\perp KH\) và \(A'B'\perp AH\) nên \(A'B'\perp\left(AHK\right)\)
\(\Rightarrow A'B'\perp HL\)
Mà \(HL\perp AK\) nên \(HL\perp\left(AA'B\right)\) \(\Rightarrow\left(AHK\right)\perp\left(AA'B\right)\)
Hơn nữa có \(AH\perp\left(A'B'C'\right)\) nên \(\left(AHK\right)\perp\left(A'B'C'\right)\)
Do đó góc nhị diện \(\left[A,A'B',C'\right]\) chính là \(\widehat{AKH}\)
Ta có \(\dfrac{1}{HK^2}=\dfrac{1}{HA'^2}+\dfrac{1}{HB'^2}\) \(=\dfrac{1}{\left(\dfrac{a\sqrt{3}}{2}\right)^2}+\dfrac{1}{\left(\dfrac{a}{2}\right)^2}\) \(=\dfrac{16}{3a^2}\)
\(\Rightarrow HK=\dfrac{a\sqrt{3}}{4}\)
\(\Rightarrow\widehat{AKH}=\tan^{-1}\left(\dfrac{AH}{KH}\right)\) \(=\tan^{-1}\left(\dfrac{\dfrac{3a}{2}}{\dfrac{a\sqrt{3}}{4}}\right)\) \(=\tan^{-1}\left(2\sqrt{3}\right)\) \(\approx73,9^o\)
Vậy ...
c) Gọi M là trung điểm BC. Khi đó dễ thấy tứ giác AMHA' là hình bình hành. Kẻ \(AX\perp HM\) tại X.
Ta có \(BC\perp AM\) và \(BC\perp AH\) nên \(BC\perp\left(AMH\right)\)
\(\Rightarrow BC\perp AX\). Lại có \(AX\perp HM\) nên \(AX\perp\left(BB'C'\right)\)
\(\Rightarrow\left(AA'HM\right)\perp\left(BB'C'\right)\)
Hơn nữa vì \(AH\perp\left(A'B'C'\right)\) nên \(\left(AA'HM\right)\perp\left(A'B'C'\right)\)
Do đó góc nhị diện \(\left[B,B'C',A'\right]\) chính là \(\widehat{A'HM}=90^o+\widehat{AHM}=90^o+\widehat{A'AH}=90^o+30^o=120^o\)
d) \(S_đ=\dfrac{a^2\sqrt{3}}{4}\)
\(\Rightarrow V_{lt}=S_đ.h\) \(=\dfrac{a^2\sqrt{3}}{4}.\dfrac{3a}{2}\) \(=\dfrac{3a^2\sqrt{3}}{8}\) (đvtt)