Chứng tỏ A là số tự nhiên biết A=1+\(\dfrac{1}{2^2}\)+\(\dfrac{1}{3^2}\)+…..+\(\dfrac{1}{2023^2}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(B=\dfrac{1}{2^2}+\dfrac{1}{3^2}+\dfrac{1}{4^2}+\dfrac{1}{5^2}+...+\dfrac{1}{2023^2}\) chứng tỏ B<1

Có : `1/2^2<1/(1*2)`
\(\dfrac{1}{3^2}< \dfrac{1}{2\cdot3}\\ ...\\ \dfrac{1}{2023^2}< \dfrac{1}{2022\cdot2023} \)
nên \(B=\dfrac{1}{2^2}+\dfrac{1}{3^2}+\dfrac{1}{4^2}+...+\dfrac{1}{2023^2}< \dfrac{1}{1\cdot2}+\dfrac{1}{2\cdot3}+\dfrac{1}{3\cdot4}+...+\dfrac{1}{2022\cdot2023}\\ =1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+...+\dfrac{1}{2022}-\dfrac{1}{2023}\\ =1-\dfrac{1}{2023}=\dfrac{2022}{2023}< 1\\ \Rightarrow B< 1\left(đpcm\right)\)

b: =>\(\dfrac{2}{2}+\dfrac{2}{6}+\dfrac{2}{12}+...+\dfrac{2}{n\left(n+1\right)}=\dfrac{200}{101}\)
=>\(\dfrac{1}{2}+\dfrac{1}{6}+\dfrac{1}{12}+...+\dfrac{1}{n\left(n+1\right)}=\dfrac{100}{101}\)
=>1-1/2+1/2-1/3+...+1/n-1/n+1=100/101
=>1-1/(n+1)=100/101
=>1/(n+1)=1/101
=>n+1=101
=>n=100

A=1/2+1/3+..+1/2019 < 1>
A= 1+1/2+1/3+..+1/2019 < 1>
A=1+1/2+1/3+..+1/2019 <1>
A=1+1/2+1/3+..+1/2019 <2018>
Vì 2018/2019 <1>
nên A=1/2+1/3+..+1/2019<1>
=> A=1/2+1/3+..+1/2019 không phải là số tự nhiên.
Mình chưa hiểu cách bạn làm với dấu <1> cho lắm.
Theo mình hiểu thì bạn đang chứng minh $A< 1$ nên $A$ không phải số tự nhiên. Mà điều này thì sai vì $A=1+(\frac{1}{2}+\frac{1}{3}+...)$ hiển nhiên lớn hơn $1$.

\(S=\left(1-\dfrac{1}{4}\right)+\left(1-\dfrac{1}{9}\right)+\left(1-\dfrac{1}{16}\right)+...+\left(1-\dfrac{1}{n^2}\right)\\ S=\left(1+1+...+1\right)-\left(\dfrac{1}{4}+\dfrac{1}{9}+...+\dfrac{1}{n^2}\right)\\ S=n-1-\left(\dfrac{1}{4}+\dfrac{1}{9}+...+\dfrac{1}{n^2}\right)< n-1\)
Lại có \(\dfrac{1}{4}+\dfrac{1}{9}+..+\dfrac{1}{n^2}=\dfrac{1}{2^2}+\dfrac{1}{3^2}+...+\dfrac{1}{n^2}\)
\(\Rightarrow\dfrac{1}{4}+\dfrac{1}{9}+...+\dfrac{1}{n^2}< \dfrac{1}{1.2}+\dfrac{1}{2.3}+...+\dfrac{1}{n\left(n-1\right)}< 1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{n-1}-\dfrac{1}{n}=1-\dfrac{1}{n}< 1\)
\(\Rightarrow S>n-1-1=n-2\\ \Rightarrow n-2< S< n-1\\ \Rightarrow S\notin N\)

a) Gọi ƯCLN(12n+1,30n+2) là d
12n+1⋮d ⇒ 60n+5⋮d
30n+2⋮d ⇒ 60n+4⋮d
(60n+5)-(60n+4)⋮d
1⋮d
Vậy \(\dfrac{12n+1}{30n+2}\) là ps tối giản
b) Đặt A=\(\dfrac{1}{2^2}+\dfrac{1}{3^2}+...+\dfrac{1}{100^2}\)
Ta có: \(\dfrac{1}{2^2}< \dfrac{1}{1.2};\dfrac{1}{3^2}< \dfrac{1}{2.3};...;\dfrac{1}{100^2}< \dfrac{1}{99.100}\)
\(A< \dfrac{1}{1.2}+\dfrac{1}{2.3}+...+\dfrac{1}{99.100}\)
\(A< 1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{99}-\dfrac{1}{100}\)
\(A< 1-\dfrac{1}{100}\)
\(A< 1-\dfrac{1}{100}< 1\left(đpcm\right)\)
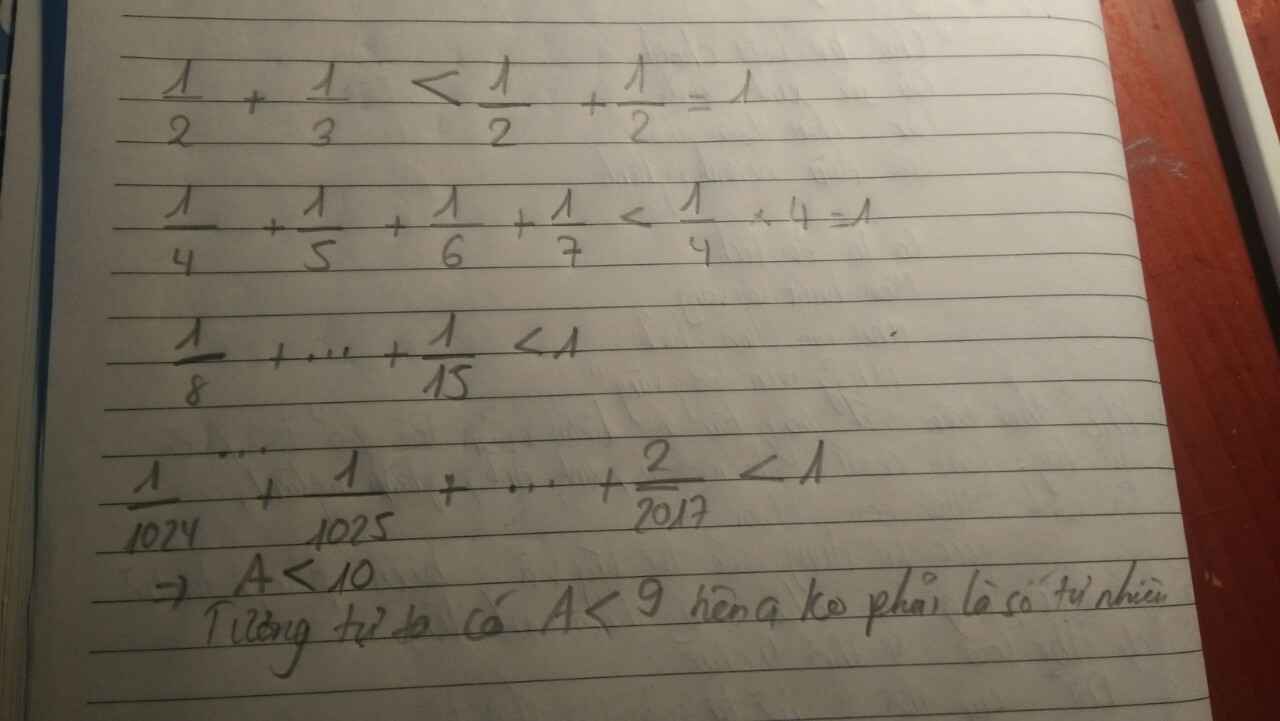
help