cho 3 điểm A(2;3), B(-1;-1), c(-3;1)
tìm tọa độ diểm D để tứ giác ABCD là hình bình hành. Tìm tọa độ tâm I của hình bình hành ABCD
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
30 tháng 3 2023
cậu có phải là Trí Kiên học thêm cùng cô Liên với tớ không , tớ là Chu Đình Gia Phúc đây
CM
29 tháng 10 2017
Gọi d: y = ax + b là đường thẳng đi qua A và B
A ( 0 ; 3 ) ∈ ( d ) ⇔ a . 0 + b = 3 ⇔ b = 3 B ( 2 ; 2 ) ∈ ( d ) ⇔ a . 2 + b = 2 ⇒ b = 3 2 a + b = 2 ⇔ b = 3 a = − 1 2 ⇒ d : y = − 1 2 x + 3
Để 2 điểm A, B, C thẳng hàng thì C ( m + 3 ; m ) ∈ ( d ) y = − 1 2 x + 3
⇔ m = − 1 2 ( m + 3 ) + 3 ⇔ 3 2 m = 3 2 ⇒ m = 1
Vậy m = 1
Đáp án cần chọn là: A
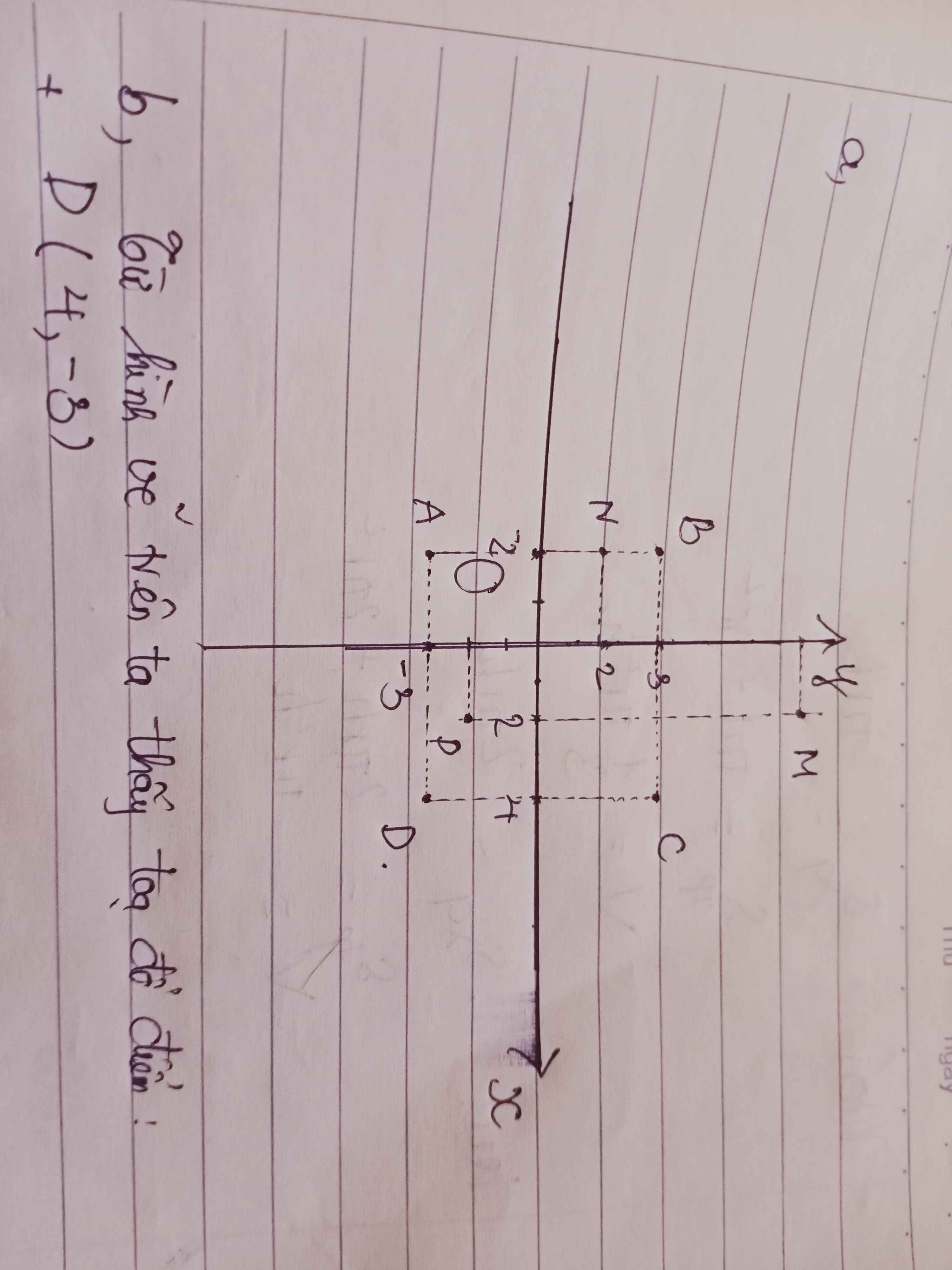
A(2;3); B(-1;-1); C(-3;1); D(x;y)
\(\overrightarrow{AB}=\left(-3;-4\right);\overrightarrow{DC}=\left(-3-x;1-y\right)\)
ta có: ABCD là hình bình hành
=>\(\overrightarrow{AB}=\overrightarrow{DC}\)
=>\(\left\{{}\begin{matrix}-3-x=-3\\1-y=-4\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x+3=3\\y-1=4\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=0\\y=5\end{matrix}\right.\)
Vậy: D(0;5)
Tọa độ tâm I của hình bình hành ABCD là:
\(\left\{{}\begin{matrix}x_I=\dfrac{x_A+x_C}{2}=\dfrac{2+\left(-3\right)}{2}=-\dfrac{1}{2}\\y_I=\dfrac{3+1}{2}=\dfrac{4}{2}=2\end{matrix}\right.\)
vậy: I(-0,5;2)