Chứng tỏ rằng số có dạng abcabc ( có gạch ngang trên đầu)bao giờ cũng chia hết cho 11
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có: \(\overline{abcabc}=\overline{abc}.1000+\overline{abc}=\overline{abc}.\left(1000+1\right)\)
\(\Rightarrow\overline{abc}.1001=\overline{abc}.91.11\)
Vì \(11⋮11\Rightarrow\overline{abc}.91.11⋮11\)
Vậy số \(\overline{abcabc}\) lúc nào cũng chia hết cho 11

a ) aaa=a.111=a.(3.37)
=>aaa bao giờ cũng chia hết cho 37
b) aaaaaa=a.111111=a.(3.37037)
=> aaaaaa bao giờ cũng chia hết cho 3
c) abcabc=abc.1001=abc.(7.13.11)
=> abcabc bao giờ cũng chia hết cho 13;11
d) ab+ba=(10a+b)+(10b+a)=(10a+a)+(10b+b)=11a+11b
=> ab+ba chia hết cho 11
ủng hộ nha
a) aaa = 111a = 37 . 3 . a
b) aaaaaa = 111111a = 37037 . 3 . a
c) abcabc = 1001abc = 77.13 . abc
abcabc = 1001abc = 77.13.abc = 7 .11.13.abc
d) (ab + ba) = 10a + b + 10b + a =11a + 11b = 11.(a+b)

Tó biết làm mỗi 2 bài trên thui
1 ) aaa aaa = a . 111 111 = a . 11 . 10101 => chia hết cho 11
2 ) abc abc = abc . 1001 = abc . 11 . 91 = > chia hết cho 11
làm theo cách thầy dạy chứ hoàn toàn ko nhìn sách giải nhé

a) Ta có: aaa=a.111
=a.3.37 chia hết cho 37
b)Ta có: ab-ba=(10a+b)-(10b+a)
=(10a-a)-(10b-b)
=9a-9b
=9(a-b) chia hết cho 9 (đpcm)
a) Ta có:
aaa = 100a + 10a + a
= 111a
= 3.37.a chia hết cho 37
b) Ta có:
ab - ba = (10a + b) - (10b + a)
= 10a + b - 10b - a
= 9a - 9b
= 9.(a - b) chia hết cho 9

abc abc=abc.1000+abc=abc.(1000+1)
=abc.1001=abc.91.11
vì 11 chia hết cho 11=>abc.91.11 chia hết cho 11
vậy số abcabc lúc nào cũng chia hết cho 11

ta có aaaaaa=100000.a+10000a+1000a+100a+10a+1
=111111a
mà 111111:7=15873
=> aaaaaa:7=15873a
=>aaaaaa chia hết cho 7
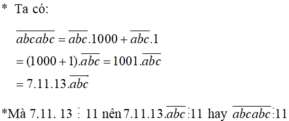

abcabc=abc.1001=abc.91.11 chia hết cho 11
tich dung cho minh nha
abcabc = 1001 x abc
= 11 x 91 x abc
luôn luôn chia hết cho 11