1 thẻ vàng + 1 thẻ vàng =?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
17 tháng 2 2019
khi trong đá bóng cầu thủ chơi bẩn
HQ
Hà Quang Minh
Giáo viên
27 tháng 9 2023
a) Các kết quả có thể xảy ra trong 2 lần lấy tấm thẻ từ 2 hộp được thể hiện ở sơ đồ hình cây như hình dưới đây:
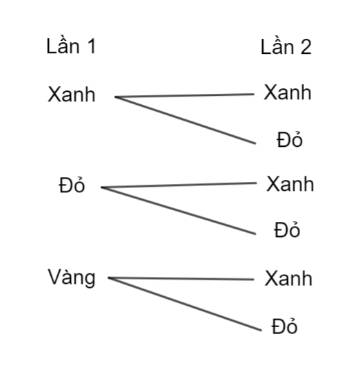
b)
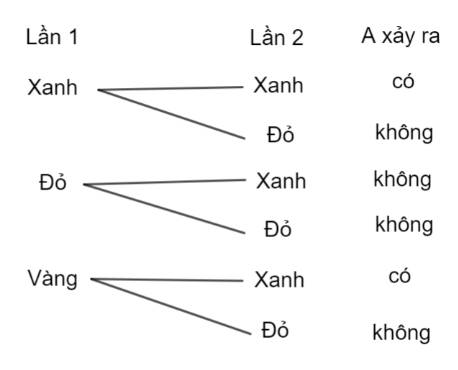
Gọi A là biến cố “Trong 2 thẻ lấy ra không có thẻ màu đỏ nào” là biến cố đối của biến cố “Trong 2 thẻ lấy ra có ít nhất 2 thẻ màu đỏ”
Dựa vào sơ đồ hình cây ta thấy có tất cả 6 kết quả có thể xảy ra, trong đó có 2 kết quả thuận lợi cho I. Do đó: \(P(A) = \frac{2}{6} = \frac{1}{3}\)
Vậy xác suất của biến cố “Trong 2 thẻ lấy ra có ít nhất 2 thẻ màu đỏ” là \(1 - \frac{1}{3} = \frac{2}{3}\)
NK
8
HQ
Hà Quang Minh
Giáo viên
1 tháng 10 2023
a) Kí hiệu \({X_1},{X_2},...,{X_7}\) là bảy thẻ màu xanh, \({D_1},{D_2},...,{D_5}\) là 5 thẻ màu đỏ và \({V_1},{V_2}\) là hai thẻ màu vàng.
Ta có không gian mẫu là \(\Omega = \left\{ {{X_1},{X_2},...,{X_7},{D_1},{D_2},...,{D_5},{V_1},{V_2}} \right\}\).
b) Ta có \(A = \left\{ {{D_1},{D_2},{D_3},{D_4},{D_5},{V_1},{V_2}} \right\},B = \left\{ {{X_2},{X_3},{D_2},{D_3},{V_2}} \right\}\).
CM
17 tháng 12 2017
Đáp án D
+ Nếu các thẻ vàng nằm ở vị trí lẻ thì các thẻ đỏ nằm ở vị trí chẵn
ta có. 7!.7! cách xếp khác nhau
+ Nếu các thẻ vàng nằm ở vị trí chẵn thì các thẻ đỏ nằm ở vị trí lẻ
ta có. 7!.7! cách xếp khác nhau
Vậy có tất cả
CM
18 tháng 6 2018
Đáp án D
+ Nếu các thẻ vàng nằm ở vị trí lẻ thì các thẻ đỏ nằm ở vị trí chẵn
ta có. 7!.7! cách xếp khác nhau
+ Nếu các thẻ vàng nằm ở vị trí chẵn thì các thẻ đỏ nằm ở vị trí lẻ
ta có. 7!.7! cách xếp khác nhau
Vậy có tất cả:
7!.7!+7!.7! = 50803200 cách
CM
15 tháng 7 2019
+ Nếu các thẻ vàng nằm ở vị trí lẻ thì các thẻ đỏ nằm ở vị trí chẵn, ta có. 7!.7! cách xếp khác nhau
+ Nếu các thẻ vàng nằm ở vị trí chẵn thì các thẻ đỏ nằm ở vị trí lẻ, ta có. 7!.7! cách xếp khác nhau
Vậy có tất cả 7! . 7! + 7! . 7! = 50803200 cách
Đáp án cần chọn là D
1 thẻ đỏ
2 the vang