cho tam giác A'B'C' đồng dạng với tam giác ABC, biết góc A=48º, góc B=54º, AB=6cm, AC=8cm, BC=9cm và A'B'=12cm. Tính : a) các góc của tam giác A'B'C' b) A'C' và B'C'
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


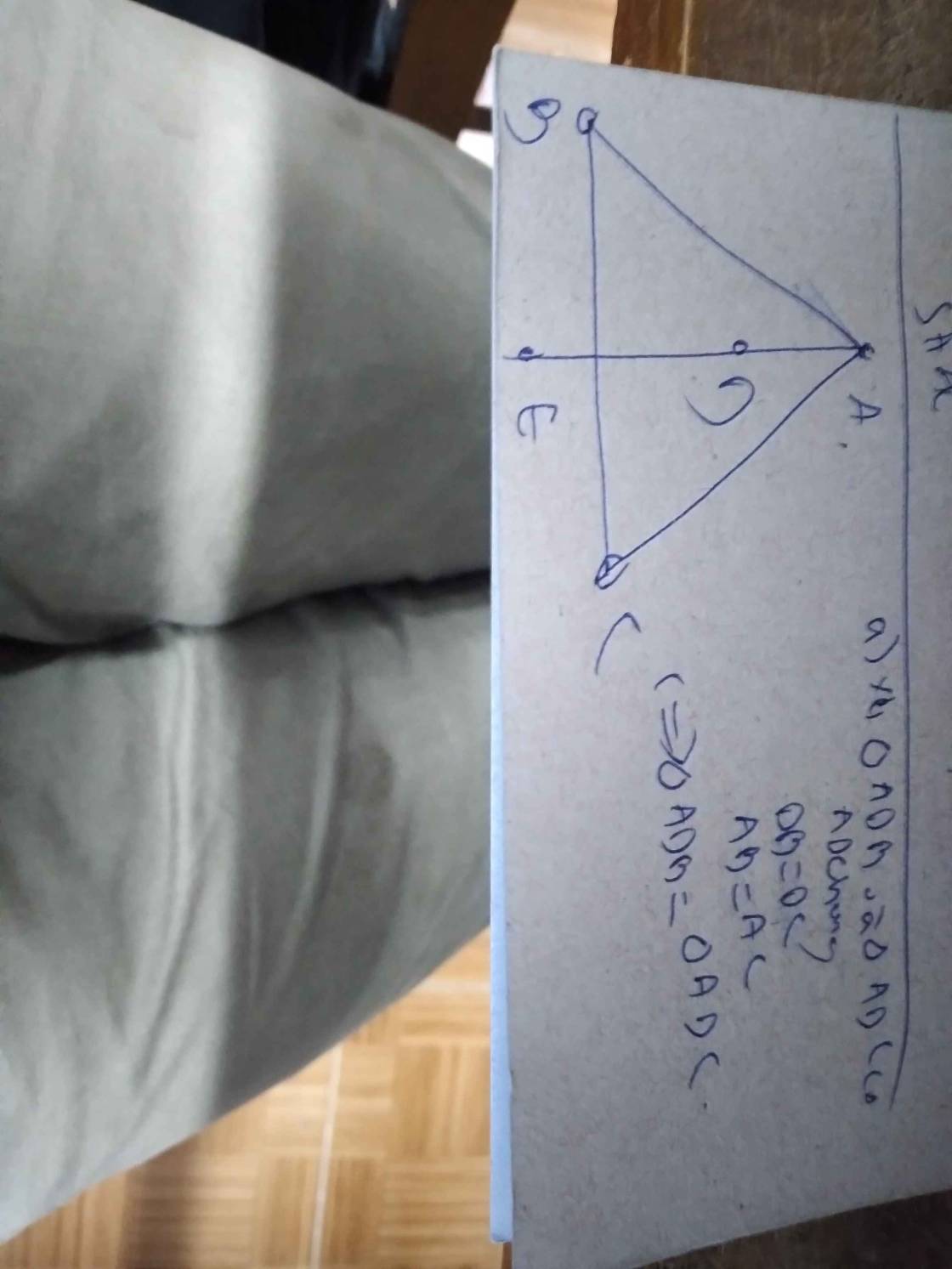
a: Xét ΔAEC và ΔAFB có
AE=AF
góc EAC chung
AC=AB
=>ΔAEC=ΔAFB
b: AE+EB=AB
AF+FC=AC
mà AE=AF và AB=AC
nên EB=FC
Xét ΔEBC và ΔFCB có
EB=FC
góc EBC=góc FCB
BC chung
=>ΔEBC=ΔFCB

a: Xét ΔBMC và ΔDMA có
MB=MD
góc BMC=góc DMA
MC=MA
=>ΔBMC=ΔDMA
=>góc MBC=góc MDA
=>BC//AD
b: Xét tứ giác ABCD có
M là trung điểm chung của AC và BD
=>ABCD là hbh
=>AB=CD=CA và AD=BC
b,c: Đề sai rồi bạn

Bài 1:
a: Xét ΔABC có \(AC^2=AB^2+BC^2\)
nên ΔABC vuông tại B
b: XétΔABC có BC<AB<AC
nên \(\widehat{A}< \widehat{C}< \widehat{B}\)

a: Xét ΔABD và ΔACD có
AB=AC
\(\widehat{BAD}=\widehat{CAD}\)
AD chung
Do đó; ΔABD=ΔACD
b: Xét ΔDBC có DB=DC
nên ΔDBC cân tại D
hay \(\widehat{DBC}=\widehat{DCB}\)
Sửa đề chứng minh tam giác ABC = tam giác ACD => △ABD = △ACD
Xét △ABD và △ACD có
AB = AC
AD là cạnh chung
\(\widehat{BAD}=\widehat{CAD}\)
nên △ABD = △ACD (c-g-c)
b)
Ta có:
\(\text{△ABD = △ACD }\)
\(\text{=> DB = DC}\)
\(\text{=> △DBC cân tại D}\)
\(=>\)\(\widehat{DBC}=\widehat{DCB}\)

a: Xét ΔHBA vuông tại H và ΔABC vuông tại A có
góc B chung
Do đó: ΔHBA∼ΔABC
b: Xét ΔHCA vuôg tại H và ΔACB vuông tại A có
góc C chung
Do đó: ΔHCA∼ΔACB

* Theo mình thì phần a) Góc A = 90 độ sẽ hợp lý hơn chứ. Vậy nên mình sẽ làm theo cả hai góc A 90 độ và 80 độ nhé ( Nhưng bài của mình phần b) sẽ theo góc A = 90 độ )
a)
Góc A = 80 độ thì sẽ có thể tam giác ABC là tam giác cân, tam giác ⊥ tại B hoặc C, tam giác ABC là tam giác tù hoặc tam giác nhọn
Góc A = 90 độ thì tam giác ABC là tam giác vuông tại A
b)
Theo phần a), ta có: Tam giác ABC cân tại A
=> Góc B = góc C = ( 180 độ - 70 độ ) : 2 = 55 độ

a) Do tam giác \(ABC\) cân tại A nên:
\(\Rightarrow\widehat{ABC}=\widehat{ACB}\) và \(AB=AC\)
Xét \(\Delta BEC\) vuông tại E và \(\Delta CFB\) vuông tại F ta có:
\(\widehat{ECB}=\widehat{FBC}\) (cmt)
Cạnh BC chung
\(\Rightarrow\Delta BEC=\Delta CFB\) (cạnh huyền, góc nhọn)
b) Do \(\Delta BEC=\Delta CFB\) (cmt) \(\Rightarrow EB=FC\) (hai cạnh tương ứng)
Ta lại có: \(AB=AC\)
\(\Rightarrow AB-FB=AC-EC\) hay \(AF=AE\)
Xét \(\Delta AHF\) vuông tại F và \(\Delta AHE\) vuông tại E ta có:
\(AF=AE\left(cmt\right)\)
Cạnh AH chung
\(\Rightarrow\Delta AHF=\Delta AHE\) (cạnh huyền, cạnh góc vuông)