Phân tích các đa thức sau thành nhân tử
a2-10a+25-y2-4yz-4z2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
DT
2
Những câu hỏi liên quan
NT
2
6 tháng 10 2018
\(a^2-10a+25-y^2-4yz-4z^2\)
\(=a^2-2.a.5+5^2-y^2-2.y.2z-\left(2z\right)^2\)
\(=\left(a-5\right)^2-\left(y+2z\right)^2\)
\(=\left(a-y-2z-5\right)\left(a+y+2z-5\right)\)
AK
6 tháng 10 2018
Very easy
\(a^2-10a+25-y^2-4yz-4z^2\)
\(=\left(a-5\right)^2-\left(y+2z\right)^2\)
\(=\left(a-5-y-2z\right)\left(a-5+y+2z\right)\)
DK
2
24 tháng 10 2021
\(a,=\left(a-5\right)^2-4b^2=\left(a-2b-5\right)\left(a+2b-5\right)\\ b,=ax^2+a-a^2x-x=ax\left(a-x\right)+\left(a-x\right)=\left(ax+1\right)\left(a-x\right)\)
24 tháng 10 2021
a: \(=\left(a-5-2b\right)\left(a-5+2b\right)\)
b: \(ax^2+a-a^2x-x\)
\(=ax\left(x-a\right)-\left(x-a\right)\)
\(=\left(x-a\right)\left(ax-1\right)\)
AH
Akai Haruma
Giáo viên
19 tháng 8 2023
Lời giải:
$x^2-y^2+a^2-b^2+2ax+2by=(x^2+a^2+2ax)-(y^2+b^2-2by)$
$=(x+a)^2-(y-b)^2=(x+a-y+b)(x+a+y-b)$
1 tháng 1 2022
a: \(=x^2\left(x-y\right)+2014\left(x-y\right)=\left(x-y\right)\left(x^2+2014\right)\)
HT
1
NM
3
12 tháng 7 2021
b) \(\left(a^2+b^2\right)^2-4a^2b^2\)
\(=\left(a^2-2ab+b^2\right)\left(a^2+2ab+b^2\right)\)
\(=\left(a-b\right)^2\cdot\left(a+b\right)^2\)
c) \(a^4-b^4=\left(a-b\right)\left(a+b\right)\left(a^2+b^2\right)\)
13 tháng 1 2022
\(a,3x^2-6x+9x^2=12x^2-6x=6x\left(2x-1\right)\\ b,3x^2+5y-3xy-5x=\left(3x^2-3xy\right)-\left(5x-5y\right)=3x\left(x-y\right)-5\left(x-y\right)=\left(x-y\right)\left(3x-5\right)\\ c,3y^2-3z^2+3x^2+6xyz=3\left(y^2-z^2+x^2+2xyz\right)\\ d,x^2-25-2xy+y^2=\left(x-y\right)^2-5^2=\left(x-y-5\right)\left(x-y+5\right)\)
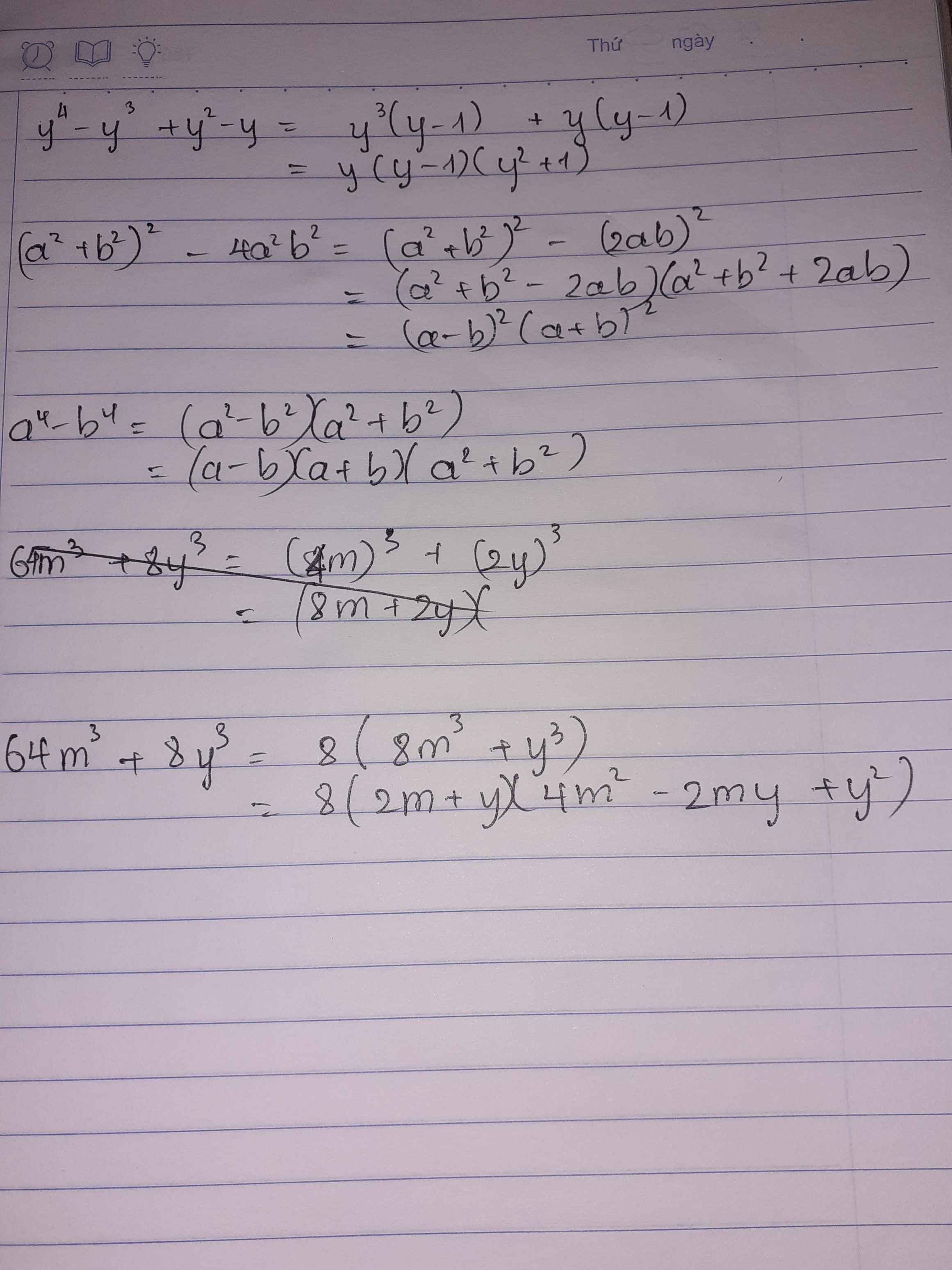
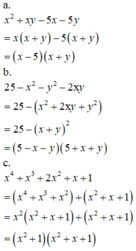
a2 - 10a + 25 - y2 - 4yz - 4z2
( a2 -10a + 52 ) - ( y2 + 4yz + 4z2 )
( a - 5 )2 - ( y + 2z )2
[ ( a - 5 ) + ( y + 2z ) ] x [ ( a - 5 ) - ( y + 2z ) ]
ở trên chỗ - ( y2 + 4yz + 4z2 ) đấy là vì tớ đặt dấu trừ trước ngoặc nên bên trong đổi dấu đấy
a) x4+x3+2x2+x+1=(x4+x3+x2)+(x2+x+1)=x2(x2+x+1)+(x2+x+1)=(x2+x+1)(x2+1)
b)a3+b3+c3-3abc=a3+3ab(a+b)+b3+c3 -(3ab(a+b)+3abc)=(a+b)3+c3-3ab(a+b+c)
=(a+b+c)((a+b)2-(a+b)c+c2)-3ab(a+b+c)=(a+b+c)(a2+2ab+b2-ac-ab+c2-3ab)=(a+b+c)(a2+b2+c2-ab-ac-bc)
c)Đặt x-y=a;y-z=b;z-x=c
a+b+c=x-y-z+z-x=o
đưa về như bài b
d)nhóm 2 hạng tử đầu lại và 2hangj tử sau lại để 2 hạng tử sau ở trong ngoặc sau đó áp dụng hằng đẳng thức dề tính sau đó dặt nhân tử chung
e)x2(y-z)+y2(z-x)+z2(x-y)=x2(y-z)-y2((y-z)+(x-y))+z2(x-y)
=x2(y-z)-y2(y-z)-y2(x-y)+z2(x-y)=(y-z)(x2-y2)-(x-y)(y2-z2)=(y-z)(x2-2y2+xy+xz+yz)