TÌM giá trị lớn nhất hay nhỏ nhất nếu có
\(B=2x^2+56x\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
25 tháng 8 2017
Ta có : x2 + 100x + 100
= x2 + 2.50.x + 2500 - 2400
= (x + 50)2 - 2400
Vì \(\left(x+50\right)^2\ge0\forall x\)
Nên : (x + 50)2 - 2400 \(\ge-2400\forall x\)
Vậy Amin = -2400 khi x = -50
15 tháng 12 2016
b) B=x-!x!
B=0 nếu x>=0
B=2x nếu x<0
=> GTLN của B=0 =0 khi x >=0
15 tháng 12 2016
a) A=!2x+6!+!2x+8!\(\ge\)I(2x+6)+(2x+8)! đảng thúc khi 2x+6 khác dau voi (2x+8)
A>=!(2x+6)-(2x+8)!=!+-2!=2
2x+6 khác dau voi (2x+8) khi -4<=x<-3
24 tháng 9 2023
Tham khảo:
Đỉnh S có tọa độ: \({x_S} = \dfrac{{ - b}}{{2a}} = \dfrac{{ - 2}}{{2.1}} = - 1;\,{y_S} = {\left( { - 1} \right)^2} + 2.( - 1) + 3 = 2.\)
Hay \(S\left( { - 1;2} \right).\)
Vì hàm số bậc hai có \(a = 1 > 0\) nên ta có bảng biến thiên sau:
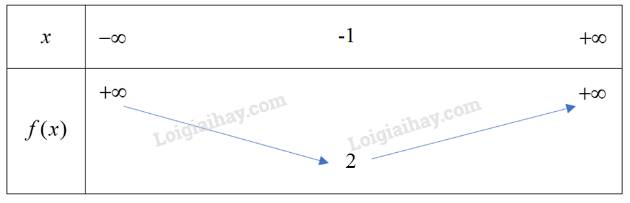
Hàm số đạt giá trị nhỏ nhất bằng \(2\).
20 tháng 8 2020
\(M=\frac{2x^2+4x+60}{x^2+2x+4}=\frac{2\left(x^2+2x+4\right)+52}{x^2+2x+4}=2+\frac{52}{x^2+2x+4}=2+\frac{52}{\left(x+1\right)^2+3}\)
Để M đạt GTNN => \(\frac{52}{\left(x+1\right)^2+3}\)đạt GTLN
=> \(\left(x+1\right)^2+3\)(*) đạt GTNN
\(\left(x+1\right)^2\ge0\forall x\Rightarrow\left(x+1\right)^2+3\ge3\)
=> Min(*) = 3 <=> x + 1 = 0 => x = -1
=> MinM = \(2+\frac{52}{\left(-1+1\right)^2+3}=2+\frac{52}{3}=\frac{58}{3}\), đạt được khi x = -1
Mình không chắc nha -.-
PN
20 tháng 8 2020
\(M=\frac{2x^2+4x+60}{x^2+2x+4}=\frac{2\left(x^2+2x+4\right)+52}{x^2+2x+4}=2+\frac{52}{x^2+2x+4}\)
Để M đạt GTLN => \(\frac{52}{x^2+2x+4}\)(**) đạt GTLN
Hay \(x^2+2x+4\)(*) đạt GTNN
Ta có : \(x^2+2x+4=\left(x^2+2x+1\right)+3=\left(x+1\right)^2+3\)
Do \(\left(x+1\right)^2\ge0\forall x\Leftrightarrow\left(x+1\right)^2+3\ge3\forall x\)
Nên GTNN (*) = 3 khi x + 1 = 0 <=> x = -1
Suy ra GTLN (**) = 52/3 khi x = -1
Vậy nên GTLN M = 2 + 52/3 = 58/3 khi x = -1
13 tháng 11 2021
\(A=\left(x^2-2x+1\right)+4=\left(x-1\right)^2+4\ge4\\ A_{min}=4\Leftrightarrow x=1\\ B=2\left(x^2-3x\right)=2\left(x^2-2\cdot\dfrac{3}{2}x+\dfrac{9}{4}\right)-\dfrac{9}{2}\\ B=2\left(x-\dfrac{3}{2}\right)^2-\dfrac{9}{2}\ge-\dfrac{9}{2}\\ B_{min}=-\dfrac{9}{2}\Leftrightarrow x=\dfrac{3}{2}\\ C=-\left(x^2-4x+4\right)+7=-\left(x-2\right)^2+7\le7\\ C_{max}=7\Leftrightarrow x=2\)
13 tháng 11 2021
a,\(A=x^2-2x+5=\left(x^2-2x+1\right)+4=\left(x-1\right)^2+4\ge4\)
Dấu "=" \(\Leftrightarrow x=-1\)
b,\(B=2\left(x^2-3x\right)=2\left(x^2-3x+\dfrac{9}{4}\right)-\dfrac{9}{2}=2\left(x-\dfrac{3}{2}\right)^2-\dfrac{9}{2}\ge-\dfrac{9}{2}\)
Dấu "=" \(\Leftrightarrow x=\dfrac{3}{2}\)
c,\(=C=-\left(x^2-4x-3\right)=-\left[\left(x^2-4x+4\right)-7\right]=-\left(x-2\right)^2+7\le7\)
Dấu "=" \(\Leftrightarrow x=2\)
LT
0
NT
2
13 tháng 9 2016
giá triwj nhỏ nhất của A = 2
B = 0
C=4
13 tháng 9 2016
A có giá trị nhỏ nhất bằng 2 khi x=-1
B có giá trị nhỏ nhất là 0 khi x=1
C có giá trị nhỏ nhất là 4 khí x=1
HL
1
26 tháng 8 2020
A = x2 + 4x + 7
= ( x2 + 4x + 4 ) + 3
= ( x + 2 )2 + 3
( x + 2 )2 ≥ 0 ∀ x => ( x + 2 )2 + 3 ≥ 3
Đẳng thức xảy ra <=> x + 2 = 0 => x = -2
=> MinA = 3 <=> x = -2
B = 2x2 - 6x
= 2( x2 - 3x + 9/4 ) - 9/2
= 2( x - 3/2 )2 - 9/2
2( x - 3/2 )2 ≥ 0 ∀ x => 2( x - 3/2 )2 -9/2 ≥ -9/2
Đẳng thức xảy ra <=> x - 3/2 = 0 => x = 3/2
=> MinB = -9/2 <=> x = 3/2
C = -2x2 + 8x - 15
= -2( x2 - 4x + 4 ) - 7
= -2( x - 2 )2 - 7
-2( x - 2 )2 ≤ 0 ∀ x => -2( x - 2 )2 - 7 ≤ -7
Đẳng thức xảy ra <=> x - 2 = 0 => x = 2
=> MaxC = -7 <=> x = 2
1 tháng 12 2021
a,Ta có B = x2-x+x = x2
Mà x2 ≥ 0 với ∀ x.Dấu ''='' xảy ra <=> x=0
Vậy Min B = 0 tại x = 0
b,Ta có 4x-x2+3 = -x2+4x-4+7
= -(x2-4x+4)+7
= -(x-2)2+7
Mà (x-2)2 ≥ 0 với ∀ 0 => -(x-2)2 ≤ 0 => -(x-2)2+7 ≤ 7
Dâu ''='' xảy ra <=> -(x-2)2 = 0 <=> x-2 = 0 <=> x=2
Vậy Max c = 7 tại x = 2.
c,Ta có 2x-2x2-5 = -x2+2x-1-x2-4
= -(x-1)2-x2-4
Mà (x-1)2 ≥ 0 => -(x-1)2 ≤ 0
x2 ≥ 0 => -x2 ≤ 0
Ta có D đạt GTLN <=> -(x-1)2 = 0 hoặc -x2 = 0
-Xét -(x-1)2 = 0 <=> x = 1. Khi đó ta có D = -5
-Xét -x2 = 0 <=> x = 0. Khi đó ta có D = -5
Vậy Max D = -5 tại x = 0 hoặc x = 1
Gtnn
\(B+392=2x^2+56x+392\)
\(B+392=2\left(x^2+28x+196\right)\)
\(B+392=2\left(x+14\right)^2\)
B+392>=0
<=> B>=-392 dau bang khi x=-14
GTln
bai nay khong co GTLN vi khi x>0 thi B tang khi x tang