cho P=1/1^2+1/2^2+1/3^2+...+1/(n-1)^2+1/n^2 chứng tỏ P<2
xin giúp mình vs ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a)M = 1 + 3 + 32 +....+ 3118 + 3119
M = (1 + 3 + 32)+(33+34+35)+...+(3117+3118+3119)
M = 1x(1+3+9)+33x(1+3+9)+...+3117x(1+3+9)
M = 1x13+33x13+...+3117x13
M = 13x(1+33+...+3117)
Vậy M chia hết cho 13

Đề là vầy đúng không bạn \(5^{n+3}-2^{n+3}+2^{n+1}-5^{n+2}+2^n\)
\(=\left(5^{n+3}-5^{n+2}\right)-\left(2^{n+3}-2^{n+1}-2^n\right)\)
\(=5^{n+2}\left(5-1\right)-2^n\left(2^3-2-1\right)\)
\(=5^{n+2}.4-2^n\left(8-2-1\right)\)
\(=5^{n+1}.2.2.5-2^{n-1}.2.5\)
\(=5^{n+1}.2.10-2^{n-1}.10\)
do \(5^{n+1}.2.10\)chia hết cho 10 với mọi n \
\(2^{n-1}.10\)chia hết cho 10 với mọi n
suy ra \(5^{n+1}.2.10-2^{n-1}.10\)chia hết cho 10 với mọi n
suy ra \(5^{n+3}-2^{n+3}+2^{n+1}-5^{n+2}+2^n\)chia hết cho 10 với mọi n

Ta có: \(\frac{1}{2^2}< \frac{1}{1.2};\frac{1}{3^2}< \frac{1}{2.3};...;\frac{1}{n^2}< \frac{1}{\left(n-1\right)n}\)
\(\Rightarrow S< \frac{1}{1.2}+\frac{1}{2.3}+...+\frac{1}{\left(n-1\right)n}=1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+...+\frac{1}{n-1}-\frac{1}{n}=1-\frac{1}{n}< 1\)
Vậy S<1
Ta có :
\(\frac{1}{2^2}+\frac{1}{3^2}+\frac{1}{4^2}+...+\frac{1}{\left(n-1\right)^2}+\frac{1}{n^2}< \frac{1}{1.2}+\frac{1}{2.3}+\frac{1}{3.4}+...+\frac{1}{\left(n-2\right)\left(n-1\right)}+\frac{1}{\left(n-1\right)n}\)
\(\Rightarrow S< 1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+...+\frac{1}{n-2}-\frac{1}{n-1}+\frac{1}{n-1}-\frac{1}{n}\)
\(\Rightarrow S< 1-\frac{1}{n}< 1\)
Vậy \(S=1\)

1/2^2<1/1*2
1/3^2<1/2*3
...
1/n^2<1/n(n-1)
Do đó; P<1-1/2+1/2-1/3+...+1/n-1-1/n=1-1/n=(n-1)/n<1

Ta có :
\(\frac{1}{2^2}< \frac{1}{1.2}\)
\(\frac{1}{3^2}< \frac{1}{2.3}\)
...................
\(\frac{1}{n^2}< \frac{1}{\left(n-1\right).n}\).
\(\Leftrightarrow\frac{1}{1^2}+\frac{1}{2^2}+....+\frac{1}{n^2}< \frac{1}{1^2}+\frac{1}{1.2}+\frac{1}{2.3}+....+\frac{1}{\left(n-1\right).n}\)
\(\Leftrightarrow\frac{1}{1^2}+\frac{1}{2^2}+...+\frac{1}{n^2}< 1+1-\frac{1}{2}+\frac{1}{2}-....+\frac{1}{n-1}-\frac{1}{n}\).
\(\Leftrightarrow\frac{1}{1^2}+\frac{1}{2^2}+...+\frac{1}{n^2}< 2-\frac{1}{n}\)
\(\Rightarrowđpcm\)
Gọi vế trái là A. Ta có: \(\frac{1}{2^2}< \frac{1}{1.2}=1-\frac{1}{2};\frac{1}{3^2}< \frac{1}{2.3}=\frac{1}{2}-\frac{1}{3};....;\frac{1}{n^2}< \frac{1}{\left(n-1\right).n}=\frac{1}{n-1}-\frac{1}{n}.\)
=> \(A< 1+1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+...+\frac{1}{n-1}-\frac{1}{n}\)
=> \(A< 2-\frac{1}{n}\) (ĐPCM)

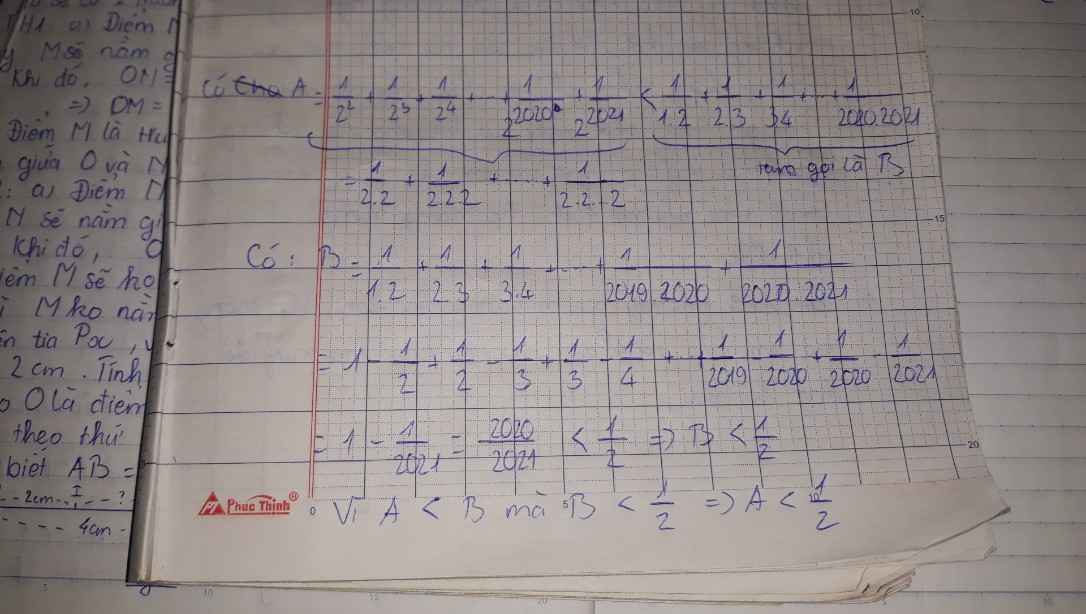
làm vào bài đừng có dùng ngoặc kép như tui nha,tui làm minh họa cho bạn hiểu
Ta có:
\(2^2>1.2\) ; \(3^2>2.3\); ....; \(n^2>\left(n-1\right)n\)
\(\Rightarrow\dfrac{1}{2^2}< \dfrac{1}{1.2}\) ; \(\dfrac{1}{3^2}< \dfrac{1}{2.3}\);...; \(\dfrac{1}{n^2}< \dfrac{1}{\left(n-1\right)n}\)
\(\Rightarrow P< \dfrac{1}{1^2}+\dfrac{1}{1.2}+\dfrac{1}{2.3}+...+\dfrac{1}{\left(n-1\right)n}\)
\(\Rightarrow P< \dfrac{1}{1^2}+\dfrac{1}{1}-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{n-1}-\dfrac{1}{n}\)
\(\Rightarrow P< 2-\dfrac{1}{n}< 2\) (đpcm)