Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Để phương trình 1 có 2 nghiệm phân biệt thì : \(\Delta>0\)
\(\Leftrightarrow\left(-4\right)^2-4\left(3-m\right)>0\\ \Leftrightarrow4+4m>0\\ \Leftrightarrow m>-1\circledast\)
Vì phương trình 1 cso hai nghiệm phân biệt
=> \(x_1=\dfrac{4-\sqrt{4+4m}}{2}\)
Theo bài ra ta có phương trình 1 cso 2 no phân biệt với \(x_1\le0\)
\(\Leftrightarrow\dfrac{4-\sqrt{4+4m}}{2}\le0\)
Mà ta có 2 > 0
\(\Rightarrow4-\sqrt{4+4m}\le0\\ \Leftrightarrow m\ge3\circledast\circledast\)
Từ * và ** thì với giá trị \(m\ge3\) thì bài toán được t/m

1.
Đặt \(\sqrt{x^2-4x+5}=t\ge1\Rightarrow x^2-4x=t^2-5\)
Pt trở thành:
\(4t=t^2-5+2m-1\)
\(\Leftrightarrow t^2-4t+2m-6=0\) (1)
Pt đã cho có 4 nghiệm pb khi và chỉ khi (1) có 2 nghiệm pb đều lớn hơn 1
\(\Leftrightarrow\left\{{}\begin{matrix}\Delta'=4-\left(2m-6\right)>0\\\left(t_1-1\right)\left(t_2-1\right)>0\\\dfrac{t_1+t_2}{2}>1\\\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}10-2m>0\\t_1t_2-\left(t_1+t_1\right)+1>0\\t_1+t_2>2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m< 5\\2m-6-4+1>0\\4>2\end{matrix}\right.\) \(\Leftrightarrow\dfrac{9}{2}< m< 5\)
2.
Để pt đã cho có 2 nghiệm:
\(\Leftrightarrow\left\{{}\begin{matrix}m\ne3\\\Delta'=1+4\left(m-3\right)\ge0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m\ne3\\m\ge\dfrac{11}{4}\end{matrix}\right.\)
Khi đó:
\(x_1^2+x_2^2=4\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=4\)
\(\Leftrightarrow\dfrac{4}{\left(m-3\right)^2}+\dfrac{8}{m-3}=4\)
\(\Leftrightarrow\dfrac{1}{\left(m-3\right)^2}+\dfrac{2}{m-3}-1=0\)
\(\Leftrightarrow\left[{}\begin{matrix}\dfrac{1}{m-3}=-1-\sqrt{2}\\\dfrac{1}{m-3}=-1+\sqrt{2}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}m=4-\sqrt{2}< \dfrac{11}{4}\left(loại\right)\\m=4+\sqrt{2}\end{matrix}\right.\)

a: Δ=(2m-1)^2-4*(-1)(m-m^2)
=4m^2-4m+1+4m-4m^2=1>0
=>(1) luôn có hai nghiệm phân biệt
b: m=x1-2x1x2+x2-2x1x2
=x1+x2-4x1x2
=2m-1+4(m-m^2)
=>m-2m+1-4m+4m^2=0
=>4m^2-5m+1=0
=>m=1 hoặc m=1/4
c: x1+x2-2x1x2
=2m-1+2m-2m^2=-2m^2+4m-1
=-2m^2+4m-2+1
=-2(m-1)^2+1<=1

Đáp án C
Phương trình ⇔ − m = x 3 − 12 x − 2 . Điều kiện trở thành đường y= m cắt đồ thị hàm số y = x 3 − 12 x − 2 tại 3 điểm phân biệt.
Lập bảng biến thiên của y = x 3 − 12 x − 2 .
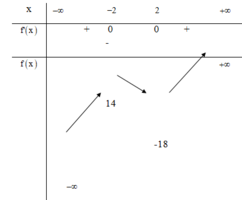
Nhìn vào bảng biến thiên, điều kiện của m là − m ∈ 14 ; − 18 ⇔ m ∈ − 14 ; 18 .

\(\Delta'=\left(m+1\right)^2-\left(m^2+2m\right)=1>0\)
\(\Rightarrow\) Phương trình luôn có 2 nghiệm: \(\left\{{}\begin{matrix}x_1=m+1-1=m\\x_2=m+1+1=m+2\end{matrix}\right.\)
\(\left|x_1\right|=3\left|x_2\right|\Leftrightarrow\left|m\right|=3\left|m+2\right|\)
\(\Leftrightarrow\left[{}\begin{matrix}3m+6=-m\\3m+6=m\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}m=-\dfrac{3}{2}\\m=-3\end{matrix}\right.\)
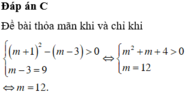



Lời giải:
Để pt có 2 nghiệm pb thì: $\Delta'=4-(3-m)>0$
$\Leftrightarrow m+1>0\Leftrightarrow m>-1(*)$
Khi đó, áp dụng định lý Viet, với $x_1,x_2$ là nghiệm của pt thì:
$x_1+x_2=4$
$x_1x_2=3-m$
Để $0\leq x_1< x_2<3$ thì:
\(x_2,x_1\geq 0\Leftrightarrow \left\{\begin{matrix}\ x_1x_2=3-m\geq 0\\ x_1+x_2=4\geq 0\end{matrix}\right.\Leftrightarrow m\leq 3(**)\)
\(x_2,x_2<3\Leftrightarrow \left\{\begin{matrix} x_1+x_2<6\\ (x_1-3)(x_2-3)>0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} 4<6\\ x_1x_2-3(x_1+x_2)+9>0\end{matrix}\right.\)
\(\Leftrightarrow 3-m-12+9>0\Leftrightarrow m<0(***)\)
Từ $(*); (**); (***)\Rightarrow -1< m< 0$