Cho tam giác cân ABC có đáy BC =a
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
15 tháng 8 2019
A B C 4 cm
Bài làm
VÌ chu vi tam giác ABC = AB + BC + CA = 16 cm
Mà Tam giác ABC cân tại A
=> AB = AC
Xét tam giác ABC có:
AB = AC = \(\frac{16-4}{2}\)= \(\frac{12}{2}\)= \(6\)
=> AB = AC > BC
Vì AB đối diện với \(\widehat{C}\)
BC đối diện với \(\widehat{A}\)
AC đối diện với \(\widehat{B}\)
Mà AB = AC > BC
=> \(\widehat{C}=\widehat{B}>\widehat{A}\)
Vậy \(\widehat{C}=\widehat{B}>\widehat{A}\)
CM
21 tháng 5 2018
Đáp án B
Gọi M là trung điểm BC
Vì các cạnh AA’ = A’B = A’C
=> Hình chiếu của A’ trên (ABC) là tâm đường tròn ngoại tiếp ∆ABC
=> A’M ⊥ (ABC)
Xét ∆A’BC, ta có A'M = a 3
Xét ∆ABC, ta có: AB = AC = a 2
Vậy 
CM
24 tháng 8 2017
Đáp án B
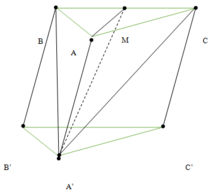
Gọi M là trung điểm BC
Vì các cạnh AA’ = A’B = A’C
ð Hình chiếu của A’ trên (ABC) là tâm đường tròn ngoại tiếp ∆ABC
ð A’M ⊥ (ABC)
Xét ∆A’BC, ta có: A’M = a 3
Xét ∆ABC, ta có: AB = AC = a 2
Vậy
V A B C . A ' B ' C ' = a 3 . S A B C = a 3 . 1 2 . a 2 . a 2 = a 3 3
17 tháng 2 2019
A C B M N 15 o 15 o
Bài làm
Vì tam giác NAB và tam giác đều
=> NA = NB = BA
=> Góc N = góc NBA = góc NAB = 60o
Ta có: Góc ABM = NAB + N ( tính chất goác ngoài tam giác )
hay Góc ABM = 60o + 60o
=> Góc ABM = 120o
Lại có: Góc ABC + CBM = ABM
hay góc ABC + 15o = 120o
=> Góc ABC = 120o - 15o
=> Góc ABC = 105o
Ta có: Góc NBM = ABN + ABC + CBM
hay góc NBM = 60o + 105o + 15o
=> góc NBM = 180o
Do đó góc NBM là góc bẹt
=> 3 điểm B, M, N thẳng hàng ( đpcm )
# Chúc bạn học tốt #
QT
Quoc Tran Anh Le
Giáo viên
22 tháng 9 2023
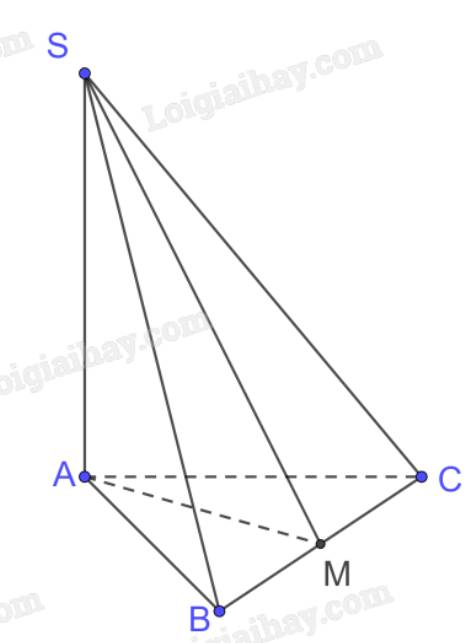
a) Xét tam giác ABC cân tại A có
AM là đường trung tuyến (M là trung điểm BC)
\( \Rightarrow \) AM là đường cao \( \Rightarrow \) \(AM \bot BC\)
Ta có:
\(\left. \begin{array}{l}AM \bot BC\\SA \bot BC\left( {SA \bot \left( {ABC} \right)} \right)\\AM \cap SA = \left\{ A \right\}\end{array} \right\} \Rightarrow BC \bot \left( {SAM} \right)\)
b) \(\left. \begin{array}{l}BC \bot \left( {SAM} \right)\\SM \subset \left( {SAM} \right)\end{array} \right\} \Rightarrow BC \bot SM\)
Xét tam giác SBC có:
+) SM là đường cao \(\left( {BC \bot SM} \right)\)
+) SM là đường trung tuyến (M là trung điểm BC)
\( \Rightarrow \) Tam giác SBC cân tại S.
??