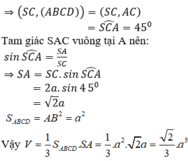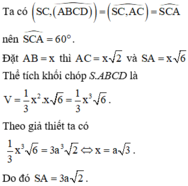Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Sửa đề; SA=SB=SC=SD=2a
SA=SB
OA=OB
=>SO là trung trực của AB
=>SO vuông góc AB(2)
SA=SD
OA=OD
=>SO là trung trực của AD
=>SO vuông góc AD(1)
Từ (1), (2) suy ra SO vuông góc (ABCD)
(SC;(ABCD))=(CS;CO)=góc SCO
\(OC=\dfrac{a\sqrt{2}}{2}\)
\(SO=\sqrt{SA^2+AO^2}\)
\(=\sqrt{\left(2a\right)^2+\left(\dfrac{a\sqrt{2}}{2}\right)^2}=\sqrt{4a^2+\dfrac{1}{2}a^2}=\dfrac{3}{\sqrt{2}}a\)
\(SC=\sqrt{SO^2+OC^2}=\sqrt{\dfrac{9}{2}a^2+\dfrac{1}{2}a^2}=a\sqrt{5}\)
\(cosSCO=\dfrac{OC}{SC}\)
\(=\dfrac{a\sqrt{2}}{2}:a\sqrt{5}=\dfrac{\sqrt{2}}{2\sqrt{5}}\)
=>\(\widehat{SCO}\simeq72^0\)
=>\(\left(SC;\left(ABCD\right)\right)=72^0\)

a.
Do AB song song DC nên góc giữa SC và AB là góc giữa SC và CD, cùng là góc SCD
Áp dụng định lý hàm cosin:
\(cos\widehat{SCD}=\dfrac{SC^2+CD^2-SD^2}{2SC.CD}=\dfrac{1}{4}\)
\(\Rightarrow\widehat{SCD}\approx75^031'\)
b.
Gọi O là tâm đáy, do chóp có đáy là hình vuông và các cạnh bên bằng nhau nên chóp là chóp đều
\(\Rightarrow SO\perp\left(ABCD\right)\)
\(\Rightarrow\Delta OAB\) là hình chiếu vuông góc của SAB lên (ABCD)
\(OA=OB=\dfrac{1}{2}AC=\dfrac{1}{2}\sqrt{AB^2+BC^2}=a\)
Mặt khác OA vuông góc OB (2 đường chéo hình vuông)
\(\Rightarrow S_{OAB}=\dfrac{1}{2}OA.OB=\dfrac{a^2}{2}\)


bị thừa nha bn tham khảo bn cần thì chép đến phần A thôi nha!

a.
Do AD song song BC nên góc giữa SD và BC là góc giữa SD và AD, cùng là góc \(\widehat{SDA}\)
Áp dụng định lý hàm cosin:
\(cos\widehat{SDA}=\dfrac{SD^2+AD^2-SA^2}{2SD.AD}=\dfrac{1}{8}\)
\(\Rightarrow\widehat{SDA}=82^049'\)
b.
Do chóp có các cạnh bên bằng nhau và đáy là hình vuông nên chóp là chóp đều
Gọi O là tâm đáy \(\Rightarrow AC\perp BD\) tại O và \(SO\perp\left(ABCD\right)\)
\(\Rightarrow\Delta OCD\) là hình chiếu vuông góc của tam giác SCD lên (ABCD)
\(OC=OD=\dfrac{1}{2}AC=\dfrac{1}{2}\sqrt{2AB^2}=a\sqrt{2}\)
\(\Rightarrow S_{OCD}=\dfrac{1}{2}OC.OD=a^2\)

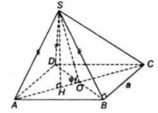
a) Tam giác ABD có AB = AD ( do ABCD là hình thoi)
=> Tam giác ABD cân tại A. Lại có góc A= 60o
=> Tam giác ABD đều.
Lại có; SA = SB = SD nên hình chóp S.ABD là hình chóp đều.
* Gọi H là tâm của tam giác ABD
=>SH ⊥ (ABD)
*Gọi O là giao điểm của AC và BD.
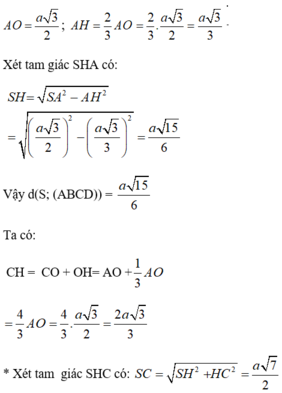



Vì SA ⊥ (ABCD) nên AC là hình chiếu vuông góc của SC lên mặt phẳng (ABCD).