Cho hình lăng trụ ABC.A'B'C'. Gọi M là trung điểm của BC; N là điểm trên cạnh CC' sao cho CN = 2 NC'
1) Tìm giao điểm I của AB với (A'MN). Tính IA/IB
2) tìm giao tuyến của (AMC') và (A'NB)
3) Tìm giao tuyến của (ANB) và (MA'C')
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A.
Phương pháp
Tính diện tích tam giác đáy và chiều cao lăng trụ suy ra thể tích theo công thức V=Bh .
Cách giải:
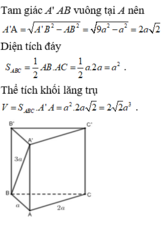
.a
Trong mp (BCC'B') nối MN kéo dài cắt BB' tại D
\(\Rightarrow D\in\left(A'MN\right)\)
Trong mp (ABB'A') nối A'D cắt AB tại I
\(\Rightarrow I=AB\cap\left(A'MN\right)\)
Do CN song song BD, áp dụng Talet:
\(\dfrac{CN}{BD}=\dfrac{CM}{BM}=1\Rightarrow CN=BD\)
\(\Rightarrow\dfrac{BD}{BB'}=\dfrac{CN}{CC'}=\dfrac{2}{3}\)
Do AA' song song BD, áp dụng Talet:
\(\dfrac{IA}{IB}=\dfrac{AA'}{BD}=\dfrac{BB'}{BD}=\dfrac{3}{2}\)
Các câu này quá nhiều đường nét nên mỗi câu 1 hình riêng cho dễ nhìn:
b.
Trong mp (ACC'A'), gọi E là giao điểm A'N và AC'
Trong mp ((BCC'B'), gọi F là giao điểm BN và C'M
\(\Rightarrow EF=\left(AMC'\right)\cap\left(A'NB\right)\)
c.
Trong mp (ACC'A'), kéo dài AN và A'C' cắt nhau tại G
\(\Rightarrow G\in\left(ANB\right)\cap\left(MA'C'\right)\)
\(F=BN\cap C'M\Rightarrow F\in\left(ANB\right)\cap\left(MA'C'\right)\)
\(\Rightarrow FG=\left(ANB\right)\cap\left(MA'C'\right)\)