Xếp hình tứ giác.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
26 tháng 3 2017
Đáp án B.
Sau khi cắt miếng giấy hình vuông như hình vẽ, ta xếp lại được thành hình chóp tứ giác đều S.MNPQ (hình bên).
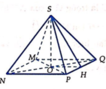Ta có
O
M
=
x
⇒
M
P
=
M
Q
=
20
M
=
2
x
=
M
N
2
⇒
M
N
=
2
x
(cm).
Gọi H là trung điểm P Q ⇒ O H = M N 2 = 2 x 2 (cm) và S H = 10 2 - 2 x 2 (cm).
Suy ra S O = S H 2 - O H 2 = 10 2 - 2 x 2 2 - 2 x 2 2 = 20 ( 10 - x ) .
Thể tích khối chóp S.MNPQ là:
V
M
N
P
Q
=
1
3
.
S
O
.
S
M
N
P
Q
=
1
3
20
(
10
-
x
)
.
2
x
2
=
20
3
(
40
-
4
x
)
.
x
4
→
V
M
N
P
Q
=
20
3
(
40
-
4
x
)
.
x
.
x
.
x
.
x
≤
20
3
40
-
4
x
+
x
+
x
+
x
+
x
5
=
256
10
3
Dấu “=” xảy ra ⇔ 40 - 4 x = x ⇔ x = 8 (cm).
CM
14 tháng 2 2018
Cách 1:
Vì tứ giác ABCD, BMNC đều là hình vuông mà tứ giác BNMC là hình bình hàng suy ra đường cao h cũng chính là cạnh BC và độ dài đáy cũng chính là cạnh DC.
Diện tích hình bình hành BMCD là:
S = a x h = DC x BC = 3 x 3 = 9 (cm2)
Đáp số: 9cm2
Cách 2: Diện tích hình bình hành BMCD bằng diện tích tam giác BCD cộng với diện tích tam giác BCM.
Tam giác BCD có đường cao BC = 3cm, cạnh đá DC = 3cm
Diện tích tam giác BCD là:
SBCD = độ dài đáy x đường cao : 2
= DC x BC : 2 = 3 x 3 : 2 = 4,5 cm2
Tam giác BCM có đường cao CB = 3cm, cạnh đáy BM = 3cm
Diện tích tam giác BCM là:
SBCM = độ dài đáy x đường cao : 2
= CB x BM : 2 = 3 x 3 : 2 = 4,5 cm2
Diện tích hình bình hành BMCD là:
S = SBCD + SBCM = 4,5 + 4,5 = 9 cm2
Cách 3:
Diện tích hình bình hành BMCD bằng diện tích nửa hình vuông ABCD + diện tích nửa hình vuông BMNC.
Diện tích nửa hình vuông ABCD có cạnh bằng 3cm là:
3 x 3 : 2 = 4,5 cm2
Diện tích nửa hình vuông BMNC có cạnh bằng 3cm là:
3 x 3 : 2 = 4,5 cm2
Diện tích hình bình hành BMCD là:
S = 4,5 + 4,5 = 9 cm2
NB
18 tháng 6 2023
Ta sử dụng phương pháp thử và sai, bắt đầu với n = 1 và tăng giá trị của n cho đến khi 1/6n(n+1)(n+2) vượt quá 100. Khi đó, n - 1 sẽ là số lớp tối đa của khối tứ diện.
Thử nghiệm:
- Với n = 1: 1/6 x 1 x 2 x 3 = 1, không vượt quá 100.
- Với n = 2: 1/6 x 2 x 3 x 4 = 4, không vượt quá 100.
- Với n = 3: 1/6 x 3 x 4 x 5 = 10, không vượt quá 100.
- Với n = 4: 1/6 x 4 x 5 x 6 = 20/3, vượt quá 100.
Vậy, số lớp tối đa của khối tứ diện được xếp từ 100 quả cam là n - 1 = 3.
Học sinh tự thực hành.