Ai giải giúp em câu 24 với ạ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
TD
4
NV
Nguyễn Việt Lâm
Giáo viên
17 tháng 9 2021
23.
Ta sẽ tìm điểm \(I\left(a;b;c\right)\) sao cho \(\overrightarrow{IA}+\overrightarrow{IB}+\overrightarrow{IC}+\overrightarrow{ID}=\overrightarrow{0}\) (1)
\(\left\{{}\begin{matrix}\overrightarrow{IA}=\left(-2-a;2-b;6-c\right)\\\overrightarrow{IB}=\left(-3-a;1-b;8-c\right)\\\overrightarrow{IC}=\left(-1-a;-b;7-c\right)\\\overrightarrow{ID}=\left(1-a;2-b;3-c\right)\end{matrix}\right.\)
\(\Rightarrow\overrightarrow{IA}+\overrightarrow{IB}+\overrightarrow{IC}+\overrightarrow{ID}=\left(-5-4a;5-4b;24-4c\right)\)
(1) thỏa mãn khi: \(\left\{{}\begin{matrix}-5-4a=0\\5-4b=0\\24-4c=0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=-\dfrac{5}{4}\\b=\dfrac{5}{4}\\c=6\end{matrix}\right.\)
\(\Rightarrow I\left(-\dfrac{5}{4};\dfrac{5}{4};6\right)\)
Khi đó:
\(T=MA^2+MB^2+MC^2+MD^2=\left(\overrightarrow{MI}+\overrightarrow{IA}\right)^2+\left(\overrightarrow{MI}+\overrightarrow{IB}\right)^2+\left(\overrightarrow{MI}+\overrightarrow{IC}\right)^2+\left(\overrightarrow{MI}+\overrightarrow{ID}\right)^2\)
\(=4MI^2+IA^2+IB^2+IC^2+ID^2+2\overrightarrow{MI}\left(\overrightarrow{IA}+\overrightarrow{IB}+\overrightarrow{IC}+\overrightarrow{ID}\right)\)
\(=4MI^2+IA^2+IB^2+IC^2+ID^2\) (do \(\overrightarrow{IA}+\overrightarrow{IB}+\overrightarrow{IC}+\overrightarrow{ID}=\overrightarrow{0}\))
\(IA^2+IB^2+IC^2+ID^2\) cố định nên \(T_{min}\) khi \(MI_{min}\)
\(\Leftrightarrow M\) trùng I
\(\Rightarrow M\left(-\dfrac{5}{4};\dfrac{5}{4};6\right)\Rightarrow x+y+z=-\dfrac{5}{4}+\dfrac{5}{4}+6=6\)
NV
Nguyễn Việt Lâm
Giáo viên
17 tháng 9 2021
24.
\(a+b=4\Rightarrow b=4-a\)
ABCD là hình chữ nhật \(\Rightarrow\overrightarrow{AB}=\overrightarrow{DC}\)
\(\Rightarrow C\left(a;a;0\right)\)
Tương tự ta có: \(C'\left(a;a;b\right)\)
M là trung điểm CC' \(\Rightarrow M\left(a;a;\dfrac{b}{2}\right)\)
\(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{A'B}=\left(a;0;-b\right)=\left(a;0;a-4\right)\\\overrightarrow{A'D}=\left(0;a;-b\right)=\left(0;a;a-4\right)\\\overrightarrow{A'M}=\left(a;a;-\dfrac{b}{2}\right)=\left(a;a;\dfrac{a-4}{2}\right)\end{matrix}\right.\)
Theo công thức tích có hướng:
\(\left[\overrightarrow{A'B};\overrightarrow{A'D}\right]=\left(-a^2+4a;-a^2+4a;a^2\right)\)
\(\Rightarrow V=\dfrac{1}{6}\left|\left[\overrightarrow{A'B};\overrightarrow{A'D}\right].\overrightarrow{A'M}\right|=\dfrac{1}{6}\left|a\left(-a^2+4a\right)+a\left(-a^2+4a\right)+\dfrac{a^2\left(a-4\right)}{2}\right|\)
\(=\dfrac{1}{4}\left|a^3-4a^2\right|=\dfrac{1}{4}\left(4a^2-a^3\right)\)
Xét hàm \(f\left(a\right)=\dfrac{1}{4}\left(4a^2-a^3\right)\) trên \(\left(0;4\right)\)
\(f'\left(a\right)=\dfrac{1}{4}\left(8a-3a^2\right)=0\Rightarrow\left[{}\begin{matrix}a=0\left(loại\right)\\a=\dfrac{8}{3}\end{matrix}\right.\)
\(\Rightarrow f\left(a\right)_{max}=f\left(\dfrac{8}{3}\right)=\dfrac{64}{27}\)
HB
1
S
21 tháng 9 2021
Xét tính trạng hình dạng cây:
\(\dfrac{Cao}{Thap}=\dfrac{9+3}{3+1}=\dfrac{3}{1}\)
=> Cao THT so với thấp
Quy ước gen: A cao. a thấp
Xét tính trạng màu sắc
\(\dfrac{Đỏ}{vang}=\dfrac{9+3}{3+1}=\dfrac{3}{1}\)
=> đỏ THT so với vàng
Quy ước gen: B đỏ. b vàng
Vì F2 thu dc tỉ lệ 9:3:3:1
=> tuân theo quy luật phân li độc lập Của Menden
=> F1 dị hợp 2 cặp giao tử. kiểu gen F1: AaBb
F1 dị hợp 2 cặp giao tử => P thuần chủng
P Cao,đỏ. x. Thấp,vàng
AABB aabb
Gp AB ab
F1: AaBb( cao,đỏ)
F1 xF1 AaBb( cao,đỏ) x AaBb( cao,đỏ)
GF1 AB,Ab,aB ab AB,Ab,aB,ab
F2: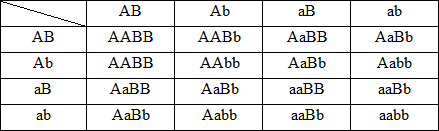
Kiểu gen: 9A_B_:3A_bb:3aaB_:1aabb
kiểu hình:9cao,đỏ :3 cao,vàng:3 thấp,đỏ:1 thấp,vàng
TN
1
25 tháng 3 2022
Câu 4.
Có \(N_1>N_2\Rightarrow\)Máy hạ thế.
Hiệu điện thế hai đầu cuộn sơ cấp:
\(\dfrac{U_1}{U_2}=\dfrac{N_1}{N_2}\Rightarrow\dfrac{1500}{250}=\dfrac{U_1}{220}\)
\(\Rightarrow U_1=1320V\)
NV
Nguyễn Việt Lâm
Giáo viên
7 tháng 1 2024
\(A=\left\{1;2;5;10;17\right\}\)
\(\left(x^2-4\right)\left(2x^2-x-1\right)=0\Rightarrow\left[{}\begin{matrix}x^2-4=0\\2x^2-x-1=0\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=\pm2\\x=1\\x=-\dfrac{1}{2}\notin Z\end{matrix}\right.\) \(\Rightarrow B=\left\{-2;1;2\right\}\)
\(\Rightarrow A\backslash B=\left\{5;10;17\right\}\)
NV
Nguyễn Việt Lâm
Giáo viên
7 tháng 1 2024
ABC vuông cân \(\Rightarrow\left\{{}\begin{matrix}AC=AB=3\\BC=AB\sqrt{2}=3\sqrt{2}\end{matrix}\right.\)
\(\overrightarrow{BC}.\overrightarrow{CA}=-\overrightarrow{CB}.\overrightarrow{CA}=-BC.AC.cos\left(\overrightarrow{CB};\overrightarrow{CA}\right)\)
\(=-3\sqrt{2}.3.cos45^0=-9\)
GN
GV Nguyễn Trần Thành Đạt
Giáo viên
13 tháng 12 2023
Bài 11:
\(PTHH:2A+Cl_2\rightarrow2ACl\\TheoĐLBTKL:\\ m_A+m_{Cl_2}=m_{ACl}\\ \Leftrightarrow 9,2+m_{Cl_2}=23,4\\ \Rightarrow m_{Cl_2}=23,4-9,2=14,2\left(g\right)\\ n_{Cl_2}=\dfrac{14,2}{71}=0,2\left(mol\right)\\ n_A=2.0,2=0,4\left(mol\right)\\ M_A=\dfrac{9,2}{0,4}=23\left(\dfrac{g}{mol}\right)\\ \Rightarrow A\left(I\right):Natri\left(Na=23\right)\)
KM
1
LN
18 tháng 10 2021
Bác mẹ là chỉ cha mẹ
Hai thân vui vầy là cha mẹ vui vẻ, hạnh phúc.
Mình biết vậy thui mong có ích cho bạn!
18 tháng 10 2021
bạn viết cho mình là mình vui rồi ! Cảm ơn bạn nhé !
I là trung điểm AB \(\Rightarrow\overrightarrow{IB}=\dfrac{1}{2}\overrightarrow{AB}\Rightarrow\overrightarrow{AB}=2\overrightarrow{IB}\)