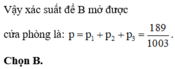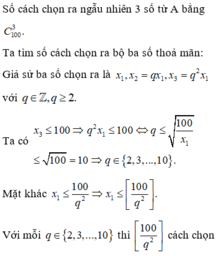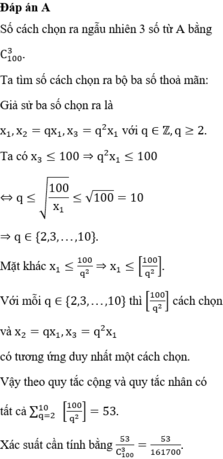Sáu số nguyên 1, 3, 5, 7, 9 và 11 tạo thành một chuỗi số học. Nếu ba trong số các số nguyên được chọn ngẫu nhiên mà không thay thế, xác suất là chúng tạo thành một dãy số học theo thứ tự chúng được chọn? Thể hiện câu trả lời của bạn dưới dạng một phân số chung.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Số phần tử của không gian mẫu là ![]()
Gọi A:”số 3 được chọn và xếp ở vị trí thứ 2”.
Trong tập đã cho có 2 số nhỏ hơn số 3, có 7 số lớn hơn số 3.
+ Chọn 1 số nhỏ hơn số 3 ở vị trí đầu có: 2 cách.
+ Chọn số 3 ở vị trí thứ hai có: 1 cách.
+ Chọn 4 số lớn hơn 3 và sắp xếp theo thứ tự tăng dần có: ![]() cách.
cách.
Do đó n(A)=2.1.35=70.
Vậy 
Chọn C.

Đáp án A
Số cách chọn ra ngẫu nhiên 3 số từ A bằng C 100 3
Ta tìm số cách chọn ra bộ ba số thoả mãn:
Giả sử ba số chọn ra là
![]()
Ta có
![]()
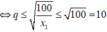
![]()
Mặt khác
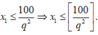
Với mỗi q ∈ 2 , 3 , . . . , 10 thì 100 q 2 cách chọn
và x 2 = q x 1 , x 3 = q 2 x 1 có tương ứng duy nhất một cách chọn.
Vậy theo quy tắc cộng và quy tắc nhân có tất cả
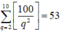
Xác suất cần tính bằng
53 C 100 3 = 53 161700