Cho parabol x^2 -4x -5 Cho A(1;3) B(4;-1), tìm C,D thuộc parabol sao cho ABCD là hình bình hành Mọi người giúp e với ạ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
13 tháng 5 2020
Gọi phương trình tiếp tuyến d tại A của parabol có dạng \(y=4x+b\) (\(b\ne5\))
Pt hoành độ giao điểm d và (P):
\(x^2=4x+b\Leftrightarrow x^2-4x-b=0\) (1)
d tiếp xúc (P) \(\Leftrightarrow\) (1) có nghiệm kép
\(\Leftrightarrow\Delta'=4+b=0\Rightarrow b=-4\)
Hoành độ giao điểm: \(x=\frac{4}{2.1}=2\Rightarrow y=4\Rightarrow A\left(2;4\right)\)
HQ
Hà Quang Minh
Giáo viên
23 tháng 9 2023
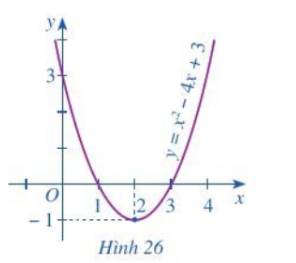
a) Từ đồ thị ta thấy bất phương trình (2) biểu diễn phần parabol (P) nằm ở phía trên trục hoành.
b) Phần parabol (P) nằm phía trên trục hoành ứng với các giá trị của x thuộc \(\left( { - \infty ;1} \right) \cup \left( {3; + \infty } \right)\)
10 tháng 4 2021
Bài 1 :
Đặt \(x^2=t\left(t\ge0\right)\)khi đó phương trình tương đương
\(t+t^2-6=0\)
Ta có : \(\Delta=1+24=25\)
\(t_1=\frac{-1-5}{2}=-3;t_2=\frac{-1+5}{2}=2\)
TH1 : \(x^2=-3\)( vô lí )
TH2 : \(x^2=2\Leftrightarrow x=\pm\sqrt{2}\)
Vậy tập nghiệm của phương trình là S = { \(\pm\sqrt{2}\)}
5 tháng 5 2021
a) \(x^2+x^4-6=0\)
Đặt \(x^2=t\left(t\ge0\right)\)
⇒ t + \(t^2\) - 6 = 0
⇒ \(t^2+t-6=0\)
⇒ Δ = \(1^2-4.\left(-6\right)\)
= 25
x1 = \(\dfrac{-1-5}{2}\) = - 3 (L)
x2 = \(\dfrac{-1+5}{2}\) = 2 (TM)
Thay \(x^2\) = 2 ⇒ x = \(\pm\sqrt{2}\)
Vậy x = \(\left\{\sqrt{2};-\sqrt{2}\right\}\)
b) (d) : y = 4x +1 - m
(p) : y = \(x^2\)
Xét phương trình hoành độ giao điểm
\(x^2=4x+1-m\)
⇒ \(x^2-4x+m-1=0\)
Δ' = 4 - m + 1
= 5 - m
Để (d) cắt (p) tại hai điểm phân biệt thì Δ' > 0
5 - m > 0
⇒ m < 5
Vậy m < 5 thì (d) cắt (p) tại hai điểm phân biệt
Gọi tọa độ giao điểm của (d) và (p) là (x1;y1) và (x2;y2)
Theo Vi-ét : \(\left\{{}\begin{matrix}S=x_1+x_2=4\\P=x_1x_2=m-1\end{matrix}\right.\)
và y1 = \(x_1^{2_{ }}\) ; y2 = \(x_2^2\)
Khi đó : \(\sqrt{y_1}.\sqrt{y_2}=5\) ⇒ \(\sqrt{y_1.y_2}=5\)
⇔ \(\sqrt{\left(x_1x_2\right)^2}=5\) ⇔ \(|m-1|=5\)
⇔ \(\left[{}\begin{matrix}m-1=5\\m-1=-5\end{matrix}\right.\) ⇔ \(\left[{}\begin{matrix}m=6\left(L\right)\\m=-4\left(TM\right)\end{matrix}\right.\)
Vậy m = - 4 thì TMĐKBT
13 tháng 2 2023
a. Theo bài ra ta có: \(x^2+x-2=0\)
\(\left[{}\begin{matrix}x=-2\\x=1\end{matrix}\right.\)\(\Rightarrow\left[{}\begin{matrix}y=-\left(-2\right)+2=4\\y=-1+2=1\end{matrix}\right.\)
Vậy tọa độ giao điểm cần tìm là: \(\left(-2;4\right)\); \(\left(1:1\right)\)
b. Thay x = 2 ; y = -1 vào hpt ta có:
\(\left\{{}\begin{matrix}8-a=b\\2+b=a\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}-a-b=-8\\-a+b=-2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=5\\b=3\end{matrix}\right.\)
NV
Nguyễn Việt Lâm
Giáo viên
6 tháng 8 2021
Parabol \(y=x^2-4x+9\) có trục đối xứng là đường thẳng \(x=-\dfrac{b}{2a}=2\)
Nên phép đối xứng trục qua đường thẳng \(x-2=0\) hay \(x=2\) sẽ cho ảnh là chính nó
Hay pt ảnh của (P) vẫn là \(x^2-4x+9\)
C,D thuộc (P) nên \(C\left(x_1;x_1^2-4x_1-5\right);D\left(x_2;x_2^2-4x_2-5\right)\)
ABCD là hình bình hành
=>\(\overrightarrow{AB}=\overrightarrow{DC}\)
\(\overrightarrow{AB}=\left(3;-4\right);\overrightarrow{DC}=\left(x_1-x_2;x_1^2-4x_1-5-x_2^2+4x_2+5\right)\)
=>\(\left\{{}\begin{matrix}x_1-x_2=3\\x_1^2-x_2^2-4x_1+4x_2=-4\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x_1-x_2=3\\\left(x_1-x_2\right)\left(x_1+x_2-4\right)=-4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_1-x_2=3\\x_1+x_2-4=-\dfrac{4}{x_1-x_2}=-\dfrac{4}{3}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x_1-x_2=3\\x_1+x_2=-\dfrac{4}{3}+4=\dfrac{12}{3}-\dfrac{4}{3}=\dfrac{8}{3}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2x_1=3+\dfrac{8}{3}=\dfrac{17}{3}\\x_1+x_2=\dfrac{8}{3}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_1=\dfrac{17}{6}\\x_2=\dfrac{8}{3}-\dfrac{17}{6}=-\dfrac{1}{6}\end{matrix}\right.\)
Khi x=17/6 thì \(y=x^2-4x-5=\left(\dfrac{17}{6}\right)^2-4\cdot\dfrac{17}{6}-5=-\dfrac{299}{36}\)
Khi x=-1/6 thì \(y=\left(-\dfrac{1}{6}\right)^2-4\cdot\dfrac{-1}{6}-5=\dfrac{1}{36}+\dfrac{2}{3}-5=-\dfrac{155}{36}\)
Vậy: \(C\left(\dfrac{17}{6};-\dfrac{299}{36}\right);D\left(-\dfrac{1}{6};-\dfrac{155}{36}\right)\)