cho hình vẽ sau:
Trong hình trên có bao nhiêu đoạn thằng song song với nhau
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

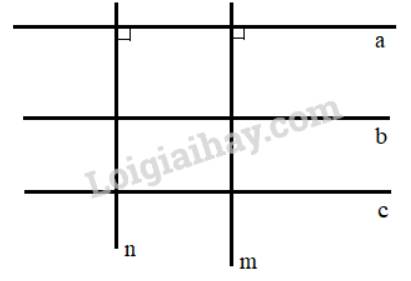
Ta có: +) a // b, b // c nên a // c ( Hai đường thẳng cùng song song với đường thẳng thứ ba thì chúng song song với nhau)
+) m \( \bot \) a; n \( \bot \)a nên m // n (Hai đường thẳng cùng vuông góc với một đường thẳng thứ ba thì song song với nhau)
Theo định lý “Đường thẳng vuông góc với 1 trong 2 đường thẳng song song thì cũng vuông góc với đường thẳng kia, ta có:
+) a // b; a \( \bot \)n nên b \( \bot \)n
+) a // b; a \( \bot \)m nên b \( \bot \)m
+) a // c; a \( \bot \)n nên c \( \bot \)n
+) a // c; a \( \bot \)m nên c \( \bot \)m
Vậy các cặp đường thẳng song song là: a // b ; a // c ; b // c; m // n
Các cặp đường thẳng vuôn góc là: b \( \bot \)n; b \( \bot \)m; c \( \bot \)n; c \( \bot \)m; a \( \bot \)n; a \( \bot \)m

Hình vẽ đã cho có:
- Cạnh AB song song với cạnh CD.
- Cạnh AB song song với cạnh MN .
- Cạnh AB song song với cạnh PQ.
- Cạnh AB song song với cạnh RT.
- Cạnh CD song song với cạnh MN.
- Cạnh CD song song với cạnh PQ.
- Cạnh CD song song với cạnh RT .
- Cạnh MN song song với cạnh PQ.
- Cạnh MN song song với cạnh PT.
- Cạnh PQ song song với cạnh RT.
Vậy trong hình đã cho có 10 cặp cạnh song song với nhau.

B A C D K O
a) Ta có BD vuông góc với AC ( 2 đường chéo của hình thoi ABCD )
=> góc BOC = góc OBK = 90 ( BK song song AC )
góc BOC = KCO = 90 (BD song song KC )
Xét tứ giác OBKC có :
góc OBK = góc BOC= góc OCK =90 ( chứng minh trên )
=> tứ giác OBKC là hình chữ nhật
b) Vì tứ giác OBKC là hình chữ nhật nên :
=> OK = BC
Mà BC= AB (cạnh của hình thoi ABCD )
=> AB = OK ( Cùng = BC )
... Đúng thì ủng hộ ạ .... ;) ;)

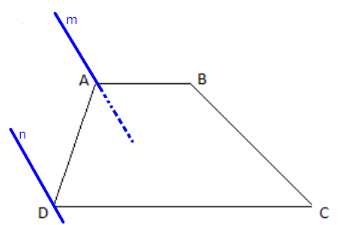
Ta có: m // n suy ra m // (C,n).
Có: AB // CD (do ABCD là hình thang) suy ra AB // (C,n).
Mặt phẳng (B,m) chứa hia đường thẳng cắt nhau m và AB song song với mp(C,n) suy ra (B,m) // (C,n).
Có 5 đoạn thẳng song song với nhau