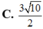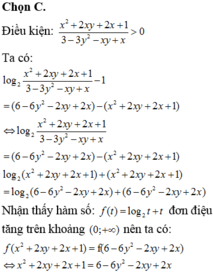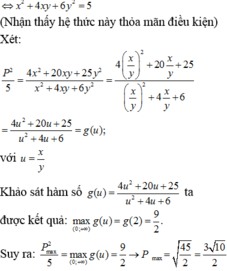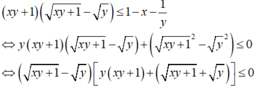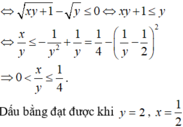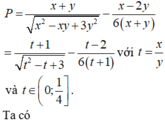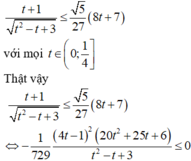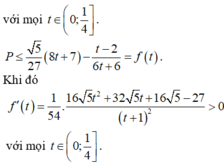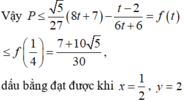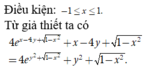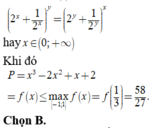Cho hai số x,y thỏa mãn x+y=2. Tìm giá trị lớn nhất của đa thức A=x2-3y2.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
9 tháng 1 2018
Đáp án B
Ta có P = 2 x 3 + y 3 - 3 x y = 2 x + y x 2 - x y + y 2 - 3 x y = 2 x + y 2 - x y - 3 x y
Mặt khác x 2 + y 2 = 2 ⇔ x + y 2 - 2 x y = 2 ⇔ 2 x y = x + y 2 - 2 ≤ x + y 2 2 ⇔ - 2 ≤ x + y ≤ 2
Khi đó 2 P = 2 x + y 4 - 2 x y - 6 x y = 2 x + y 4 - x + y 2 + 2 - 3 x + y 2 - 2
= 6 + 12 x + y - 3 x + y 2 - 2 x + y 3 = f t = 6 + 12 t - 3 t 2 - 2 t 3
Với t = x + y ∈ - 2 ; 2
Xét hàm số f t = 6 + 12 t - 3 t 2 - 2 t 3 trên đoạn [-2;2] ta có
f ' t = 12 - 6 t - 6 t 2 ; f ' t = 0 ⇔ [ t = - 2 t = 1
So sánh các giá trị f(-2);f(1);f(2), ta được m a x - 2 ; 2 f t = f 1 = 13 ⇒ M = 13 2 .
CM
1 tháng 1 2020
Ta có x + y = 2 ⇒ y = 2 - x ≥ 0 ⇒ 0 ≤ x ≤ 2 . Thay y = 2 - x và biểu thức P ta được
P = 1 3 x 3 + x 2 + 2 - x 2 - x + 1 = 1 3 x 3 + 2 x 2 - 5 x + 5 = f x
với x ∈ 0 ; 2
Đạo hàm f ' x = x 2 + 4 x - 5 = 0 ⇔ x = 1 x = - 5
Do x ∈ 0 ; 2 nên loại x = -5
f 1 = 7 3 ; f 0 = 5 ; f 2 = 17 3
Vậy m i n x ∈ 0 ; 2 P = m i n x ∈ 0 ; 2 f x = 7 3 khi và chỉ khi x = 1
Đáp án B