cho sơ đồ mạch điện như hình vẽ biết R1 = 8 ôm R2 = 20 ôm R3 = 30 ôm ampe kế chỉ 1,5 Ampe A. tính điện trở tương đương của mạch đoạn b. tính cường độ dòng điện mỗi điện trở qua mạch chính
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
8 tháng 7 2021
a)
Ta có sơ đồ mạch điện
( R2//R3)ntR1
Điện trở của đoạn mạch AB là
R23 = 10*15/10+15=6Ω
R123 = Rtđ = 6 + 4 = 10Ω
26 tháng 10 2023
a, \(R_{23}=\dfrac{R_2.R_3}{R_2+R_3}=\dfrac{30.30}{30+30}=15\left(\Omega\right)\)
\(R_{tđ}=R_1+R_{23}=15+15=30\left(\Omega\right)\)
\(b,I_1=I_{23}=I_m=\dfrac{U}{R_{tđ}}=\dfrac{12}{30}=0,4\left(A\right)\)
\(U_{23}=U_m-U_1=12-\left(0,4.15\right)=6\left(V\right)\)
\(\rightarrow I_1=I_2=\dfrac{6}{30}=0,2\left(A\right)\)
c, \(P=U.I=12.0,4=4,8\left(W\right)\)
\(Q=A.t=P.t=4,8.5.60=1440\left(J\right)\)
TK
17 tháng 12 2021
MCD: R1 nt(R2//R3)
a, ĐIện trở tương đương của đoạn mạch
\(R_{23}=\dfrac{R_2R_3}{R_2+R_3}=\dfrac{30\cdot20}{30+20}=12\left(\Omega\right)\)
\(R_{tđ}=R_1+R_{23}=18+12=30\left(\Omega\right)\)
b,Cường độ dòng điện qua mỗi điện trở
\(I_1=I_{23}=I=\dfrac{U}{R_{tđ}}=\dfrac{60}{30}=2\left(A\right)\)
\(U_2=U_3=U_{23}=I_{23}\cdot R_{23}=2\cdot12=24\left(V\right)\)
\(I_2=\dfrac{U_2}{R_2}=\dfrac{24}{30}=0,8\left(A\right)\)
\(I_3=\dfrac{U_3}{R_3}=\dfrac{24}{20}=1,2\left(A\right)\)
9 tháng 7 2023
a)
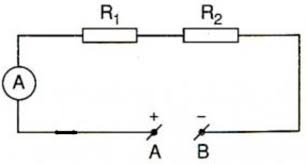
b) Điện trở tương đương là:
\(R_{tđ}=R_1+R_2=15+20=35\Omega\)
Hiệu điện thế của đoạn mạch AB là:
\(U_{AB}=I.R_{tđ}=0,4.35=14V\)
c) Cường độ dòng điện lúc sau là:
\(I'=\dfrac{U'}{R_{tđ}}=\dfrac{60}{35}=\dfrac{12}{7}A\)
Vì R1 và R2 mắc nt
\(\Rightarrow I'=I_1=I_2=\dfrac{12}{7}A\)
8 tháng 10 2021
a) Do \(R_2ntR_3\)
\(\Rightarrow R_{23}=R_2+R_3=4+6=10\left(\Omega\right)\)
Do \(R_{23}//R_1\)
\(\Rightarrow R_{tđ}=\dfrac{R_{23}.R_1}{R_{23}+R_1}=\dfrac{10.10}{10+10}=5\left(\Omega\right)\)
b) Hiệu điện thế giữa 2 đầu mạch chính:
\(U=I.R=1,5.5=7,5\left(\Omega\right)\)
Do mạch song song nên \(U=U_1=U_{23}=7,5\Omega\)
\(I_1=\dfrac{U_1}{R_1}=\dfrac{7,5}{10}=0,75\left(A\right)\)
\(I_2=I_3=I_{23}=\dfrac{U_{23}}{R_{23}}=\dfrac{7,5}{10}=0,75\left(A\right)\)
26 tháng 9 2021
a) Điện trở tương đương Rtđ(1):
\(R_{tđ\left(1\right)}=R_1+R_2=20+30=50\left(\Omega\right)\)
ĐTTĐ của mạch:
\(R_{tđ}=\dfrac{R_{tđ\left(1\right)}.R_3}{R_{tđ\left(1\right)}+R_3}=\dfrac{50.30}{50+30}=18,75\left(\Omega\right)\)
b, CĐDĐ toàn mạch:
\(I=\dfrac{U}{R}=\dfrac{60}{18,75}=3,2\left(A\right)\)
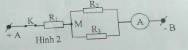
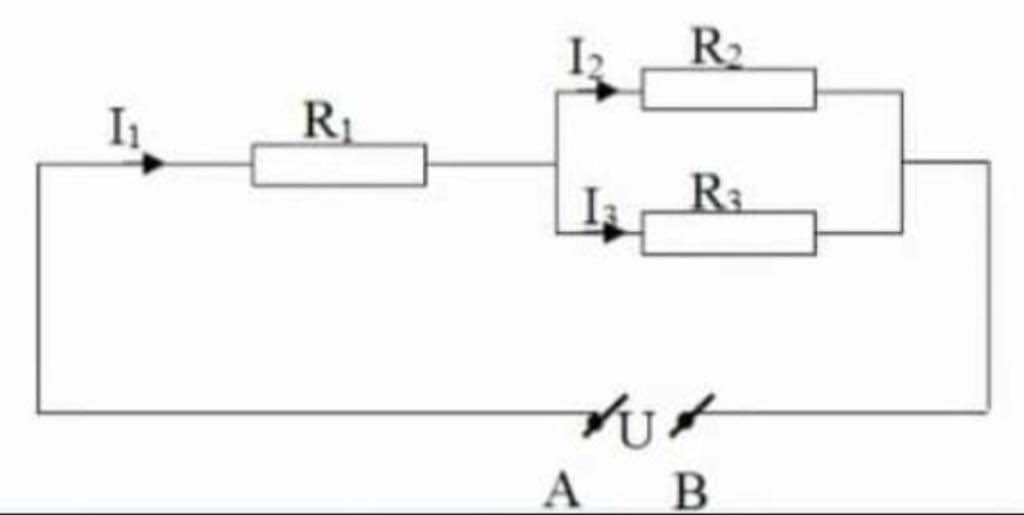
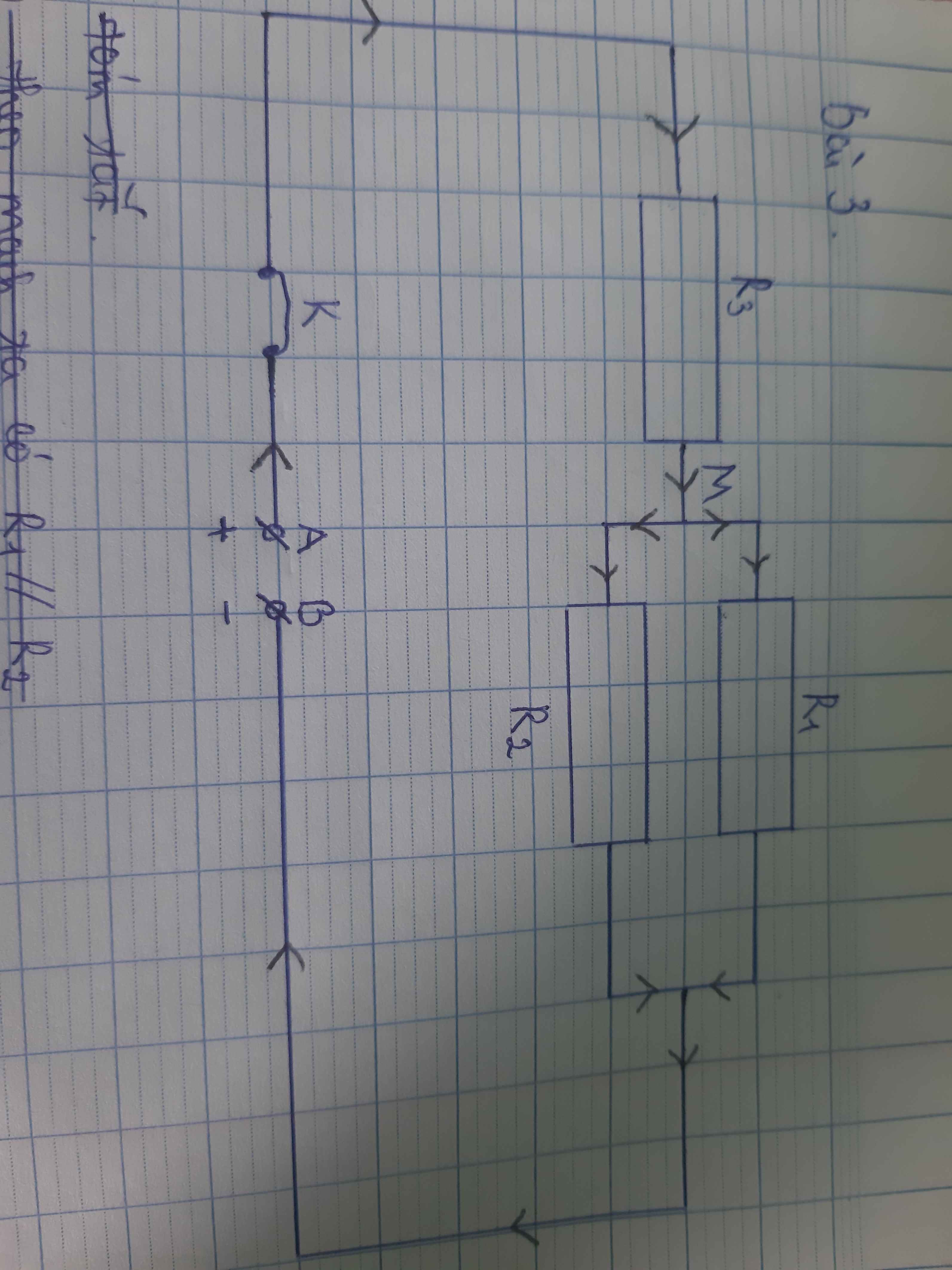
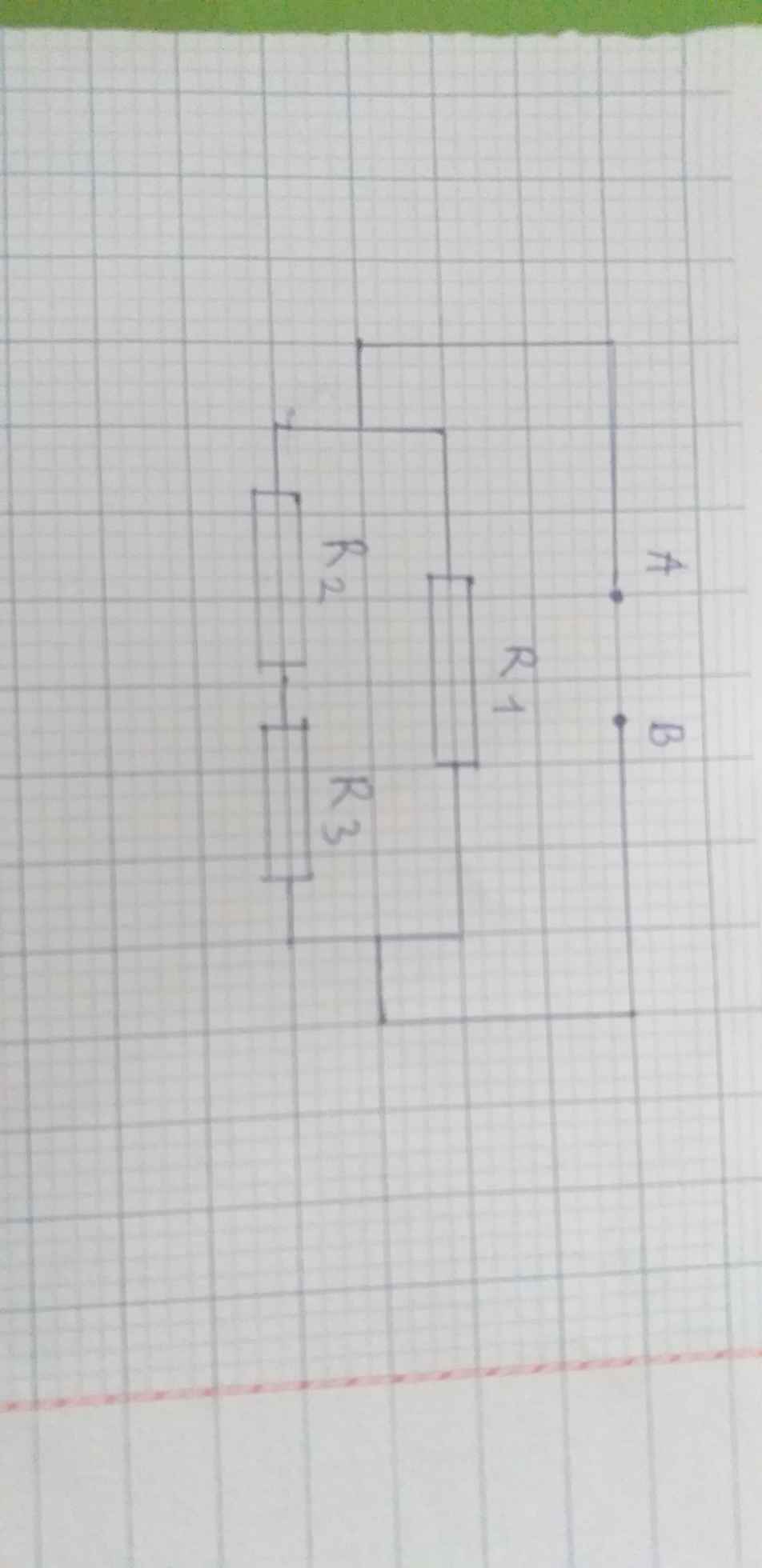
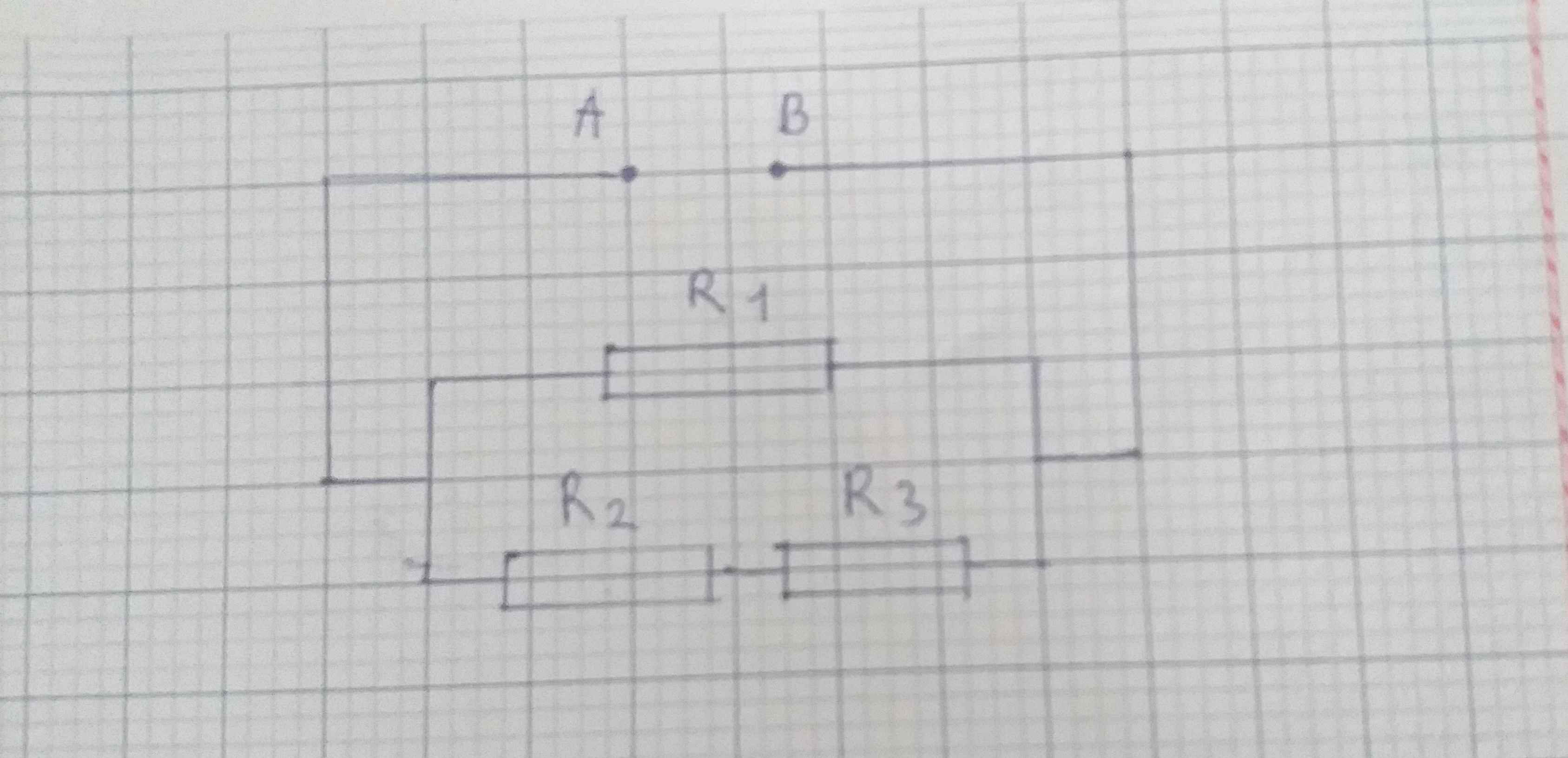cho mạch điện như hình vẽ với R1=10 ôm , R2=4 ôm, R3=6 ôm cường độ dòng điện qua mạch chính là i = 1,5 A a) tính điện trở tương đương của mạch b) tính cường độ dòng điện qua mỗi điện trở Nhanh vs ạ e cần gấp cảm ơn nhiều ạ