cho hình bình hành abcd .gọi M N theo thứ tự là trung điểm của AB và CD a. chứng minh tứ giác bmdn là hình bình hành b.chứng minh góc amd=góc bnc c gọi i là trung điểm của ac chứng minh m,i,n là thẳng hàng
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
8 tháng 11 2021
a: Xét tứ giác BMDN có
BM//DN
BM=DN
Do đó: BMDN là hình bình hành
29 tháng 12 2021
a: Xét tứ giác BMDN có
DM//BN
DM=BN
Do đó: BMDN là hình bình hành
6 tháng 9 2021
Xét tứ giác AMND có
AM//ND
AM=ND
Do đó: AMND là hình bình hành
Suy ra: MN//AD
hay MN\(\perp\)AC
Xét tứ giác AMCN có
AM//CN
AM=CN
Do đó: AMCN là hình bình hành
mà MN\(\perp\)AC
nên AMCN là hình thoi
6 tháng 9 2021
Xét tứ giác AMND có
AM//ND
AM=ND
Do đó: AMND là hình bình hành
Suy ra: MN//AD
hay MN\(\perp\)AC
Xét tứ giác AMCN có
AM//CN
AM=CN
Do đó: AMCN là hình bình hành
mà MN\(\perp\)AC
nên AMCN là hình thoi
11 tháng 11 2018
MỌI NGƯỜI GIÚP MÌNH TRONG HÔM NAY VỚI Ạ !!! MAI MÌNH KIỂM TRA RÙI !!! THANK KIU EVERYONE, MONG NHẬN ĐK CÂU TRẢ LỜI SỚM ( MÀ MỌI NGƯỜI KHÔNG CẦN VX HÌNH ĐÂU Ạ ^^)
TD
11 tháng 11 2018
1) a. xét trong tam giác ABC có
I trung điểm AB và K trung điểm AC =>IK là đường trung bình của tam giác ABC=>IK song song với BC
vậy BCKI là hình thang (vì có hai cạng đáy song song)
b.
IK // và =1/2BC (cm ở câu a) =>IK song song NM
M trung điểm HC và N trung điểm HB mà HB+HC=CB =>MN=IK=1/2BC
suy ra MKIN là hbh => có hai đường chéo bằng nhau =>IM=NK
CM
22 tháng 12 2019
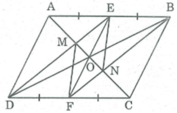
Xét ∆ EOM và ∆ FON có: ∠ (MEO) = ∠ (NFO) (so le trong do DE//BF)
OE = OF (tính chất hình bình hành)
∠ (MOE)= ∠ (NOF) (đối đỉnh )
Suy ra: ∆ EOM = ∆ FON (g.c.g) ⇒ OM = ON
Vậy tứ giác EMFN là hình bình hành (vì có hai đường chéo cắt nhau tại trung điểm mỗi đường).
6 tháng 9 2021
Xét tứ giác AMND có
AM//ND
AM=ND
Do đó: AMND là hình bình hành
Suy ra: MN//AD
hay MN\(\perp\)AC
Xét tứ giác AMCN có
AM//CN
AM=CN
Do đó: AMCN là hình bình hành
mà MN\(\perp\)AC
nên AMCN là hình thoi
⇒ BM = AM = AB : 2
Do N là trung điểm của CD (gt)
⇒ CN = DN = CD : 2
Do ABCD là hình bình hành (gt)
⇒ AB = CD và AB // CD
⇒ BM = AB : 2 = CD : 2 = DN
Do AB // CD (cmt)
⇒ BM // DN
Tứ giác BMDN có:
BM // DN (cmt)
BM = DN (cmt)
⇒ BMDN là hình bình hành
b) Do BMDN là hình bình hành (cmt)
⇒ BN // DM
⇒ ∠AMD = ∠MBN (đồng vị) (1)
Do AB // CD (cmt)
⇒ ∠MBN = ∠BNC (so le trong) (2)
Từ (1) và (2) ⇒ ∠AMD = ∠BNC
c) Do ABCD là hình bình hành
I là trung điểm của AC (gt)
⇒ I là trung điểm của BD
Do BMDN là hình bình hành (cmt)
I là trung điểm của BD (cmt)
⇒ I là trung điểm của MN
⇒ M, I, N thẳng hàng