Tìm cặp số tự nhiên (x,y) sao cho...
Đọc tiếp
Tìm cặp số tự nhiên (x,y) sao cho x2 +55=4y2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
AH
Akai Haruma
Giáo viên
27 tháng 11 2023
Lời giải:
$x^2+55=4y^2$
$4y^2-x^2=55$
$(2y-x)(2y+x)=55$
Vì $x,y$ là số tự nhiên nên $2y+x, 2y-x$ là số nguyên và $2y+x>0$.
Mà $(2y-x)(2y+x)=55>0$ nên $2y-x>0$
Kết hợp với $2y+x\geq 2y-x$ ta có các TH sau:
TH1: $2y-x=1; 2y+x=55\Rightarrow y=14; x=27$
TH2: $2y-x=5; 2y+x=11\Rightarrow y=4; x=3$
NC
1
NV
11 tháng 3 2023
\(x^2+4y^2=x^2y^2-2xy\)
\(\Rightarrow x^2+4y^2+4xy=x^2y^2+2xy+1-1\)
\(\Rightarrow\left(x+2y\right)^2=\left(xy+1\right)^2-1\)
\(\Rightarrow\left(xy+1\right)^2-\left(x+2y\right)^2=1\)
\(\Rightarrow\left(xy-x-2y+1\right)\left(xy+x+2y+1\right)=1\)
Vì x,y là các số nguyên nên \(\left(xy-x-2y+1\right),\left(xy+x+2y+1\right)\) là các ước số của 1. Do đó ta có 2 trường hợp:
TH1: \(\left\{{}\begin{matrix}xy-x-2y+1=1\\xy+x+2y+1=1\left(1\right)\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}-xy+x+2y-1=-1\\xy+x+2y+1=1\end{matrix}\right.\)
\(\Rightarrow2\left(x+2y\right)=0\Rightarrow x=-2y\)
Thay vào (1) ta được:
\(-2y^2+1=1\Leftrightarrow y=0\Rightarrow x=0\)
TH2: \(\left\{{}\begin{matrix}xy-x-2y+1=-1\\xy+x+2y+1=-1\left(1\right)\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}-xy+x+2y-1=1\\xy+x+2y+1=-1\end{matrix}\right.\)
\(\Rightarrow2\left(x+2y\right)=0\Rightarrow x=-2y\)
Thay vào (1) ta được:
\(-2y^2+1=-1\Leftrightarrow\left[{}\begin{matrix}y=1\\y=-1\end{matrix}\right.\)
\(y=1\Rightarrow x=-2;y=-1\Rightarrow x=2\)
Vậy các cặp số nguyên (x;y) thỏa điều kiện ở đề bài là \(\left(0;0\right),\left(2;-1\right)\left(-2;1\right)\)
CT
0
NV
1
21 tháng 5 2021
Áp dụng bđt bunhia có:
\(\left(x^2+4y^2\right)\left(1+\dfrac{1}{4}\right)\ge\left(x+y\right)^2\)
\(\Leftrightarrow\dfrac{25}{4}\ge\left(x+y\right)^2\)\(\Leftrightarrow x+y\le\dfrac{5}{2}\)
Dấu = xảy ra\(\Leftrightarrow\left\{{}\begin{matrix}x=4y\\x^2+4y^2=5\end{matrix}\right.\Leftrightarrow\) \(\left\{{}\begin{matrix}16y^2+4y^2=5\\x=4y\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}y=\dfrac{1}{2}\\x=2\end{matrix}\right.\)
21 tháng 11 2015
d 10^n+72^n -1
=10^n -1+72n
=(10-1) [10^(n-1)+10^(n-2)+ .....................+10+1]+72n
=9[10^(n-1)+10^(n-2)+..........................-9n+81n
GN
GV Nguyễn Trần Thành Đạt
Giáo viên
4 tháng 8 2023
a, 17x3y chia hết cho 15 => 17x3y chia hết cho 5
TH1: y=0 => Các số chia hết 15: 17130, 17430, 17730 => x=1 hoặc x=4 hoặc x=7
TH2: y=5 => Các số chia hết cho 15: 17235, 17535, 17835 => x=2 hoặc x=5 hoặc x=8
Vậy: Các cặp số (x;y) thoả mãn: (x;y)= {(1;0); (4;0); (7;0); (2;5); (5;5); (8;5)}
GN
GV Nguyễn Trần Thành Đạt
Giáo viên
4 tháng 8 2023
34x5y chia hết cho 36 => 34x5y là số chẵn và chia hết cho 3, chia hết cho 9
TH1: y=0 => Các số chia hết cho 36: Không có số thoả
TH2: y=2 => Các số chia hết cho 36: 34452 => x=4
TH3: y=4 => Các số chia hết cho 36: Không có số thoả
TH4: y=6 => Các số chia hết cho 36: 34056; 34956 => x=0 hoặc x=9
TH5: y=8 => Các số chia hết cho 36: Không có số thoả
=> Các số chia hết cho 36 tìm được: 34452; 34056 và 34956
Vậy: (x;y)={(4;2); (0;6); (9;6)}
LB
1
H9
HT.Phong (9A5)
CTVHS
4 tháng 8 2023
Để \(\overline{x73y}\) chia hết cho 4 thì \(\overline{3y}\) phải chia hết cho 4
Mà: \(\overline{3y}\) ⋮ 4 Khi \(y\in\left\{2;6\right\}\)
\(1\le x\le9\)
Để \(\overline{x73y}\) chia hết cho 5 khi \(y\in\left\{0;5\right\}\)
\(1\le x\le9\)
NP
1
20 tháng 4 2015
xy-x-y=2
xy-x-y+1=2+1
x(y-1) - (y-1)=3
(y-1)(x-1)=3
x;y nguyên
3=1.3=3.1=(-1)(-3)=(-3)(-1)
y-1 1 3 -1 -3
y 2 4 0 -2
x-1 3 1 -3 -1
x 4 2 -2 0
Vậy có những cặp x;y:
2;4
4;2
0;-2
-2;0
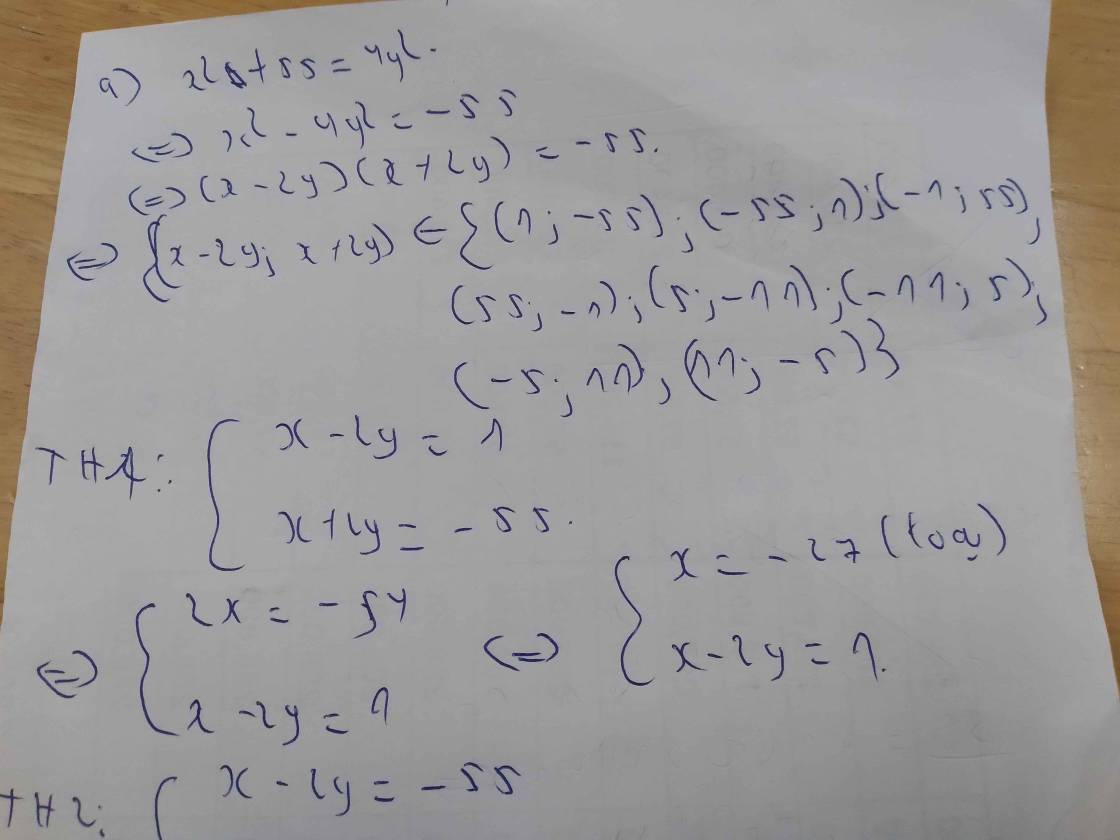
Lời giải:
$x^2+55=4y^2$
$\Leftrightarrow 55=4y^2-x^2=(2y-x)(2y+x)$
Do $x,y$ là stn nên $2y+x$ là stn.
$\Rightarrow 2y+x>0$. Mà $(2y+x)(2y-x)=55>0$ nên $2y-x>0$.
Vậy $2y+x> 2y-x>0$.
Khi đó ta có các TH sau:
TH1: $2y-x=1, 2y+x=55\Rightarrow y=14; x=27$ (tm)
TH2: $2y-x=5; 2y+x=11\Rightarrow y=4; x=3$ (tm)