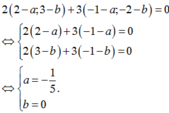Trong mặt phẳng tọa độ Oxy cho điểm M(1;2). Gọi (d) là đường thẳng thay đổi đi qua M và cắt các tia Ox, Oy lần lượt tại A,B (A, B không trùng gốc tọa độ O). Đặt S là diện tích ΔOAB. Tính giá trị nhỏ nhất của S.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
3 tháng 5 2019
Ta có P ∈ O x nên P( x; 0) và M P → = x + 2 ; − 2 M N → = 3 ; − 1 .
Do M, N, P thẳng hàng nên 2 vecto M P → ; M N → cùng phương
⇒ x + 2 3 = − 2 − 1 = 2 ⇔ x + 2 = 6 ⇔ x = 4 ⇒ P 4 ; 0 .
Chọn D.
CM
13 tháng 1 2017
Ta có P ∈ O x nên P(x; 0) và M P → = x + 2 ; − 2 M N → = 3 ; − 1 .
Do M, N, P thẳng hàng nên x + 2 3 = − 2 − 1 ⇔ x = 4 ⇒ P 4 ; 0 .
Chọn D.
CM
31 tháng 3 2019
Ta có M(x^',y') là ảnh của M qua phép tịnh tiến theo vecto v→
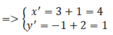
⇒ M(4;1)