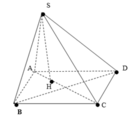
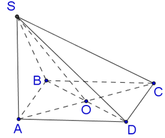
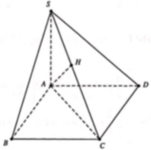
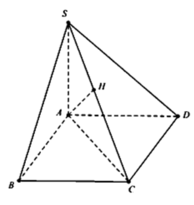
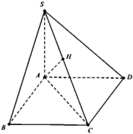
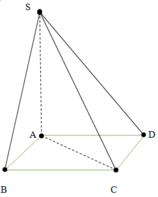
Cho hình chóp tứ giác đều S.ABCD có O là giao điểm của AC và BD. Biết \(SO=a\sqrt{2}\), góc giữa đường thẳng SA và nặt phẳng (ABCD) bằng 45o.
a) Tính thể tích khối chóp S.ABCD theo \(a\).
b) Gọi K là điểm di động trên mặt phẳng (ABCD). Tìm \(\widehat{SAK}\) để biểu thức \(T=\dfrac{SA+AK}{SK}\) đạt giá trị lớn nhất.
(Giúp mình làm câu b thôi nhé.)