Cho tam giác ABC. lấy M là trung điểm của cạnh BC. Trên tia đối của tia MA lấy điểm D sao cho MA = MD.
a, Chứng minh tam giác AMB = tam giác DMC;
b, Chứng minh AC // BD;
c, Kẻ AH vuông góc với BC, DK vuông góc với BC (H, K thuộc BC). Chứng minh BK = CH;
d, Gọi I là trung điểm của AC, vẽ điểm E sao cho I là trung điểm của BE. Chứng minh C là trung điểm của DE

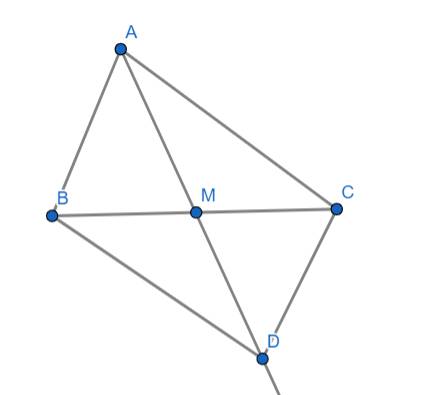

a: Xét ΔMAB và ΔMDC có
MA=MD
\(\widehat{AMB}=\widehat{DMC}\)(hai góc đối đỉnh)
MB=MC
Do đó: ΔMAB=ΔMDC
b: Xét ΔMAC và ΔMDB có
MA=MD
\(\widehat{AMC}=\widehat{DMB}\)(hai góc đối đỉnh)
MC=MB
Do đó: ΔMAC=ΔMDB
=>\(\widehat{MAC}=\widehat{MDB}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AC//BD
c: ΔMAB=ΔMDC
=>\(\widehat{MBA}=\widehat{MCD}\)
Xét ΔABH vuông tại H và ΔDCK vuông tại K có
AB=DC
\(\widehat{ABH}=\widehat{DCK}\)
Do đó: ΔABH=ΔDCK
=>BH=CK
BH+HK=BK
CK+HK=CH
mà BH=CK
nen BK=CH
d: Xét tứ giác ABCE có
I là trung điểm chung của AC và BE
=>ABCE là hình bình hành
=>AB//CE và AB=CE
Ta có: AB//CE
AB//CD
CD,CE có điểm chung là C
Do đó: C,E,D thẳng hàng
Ta có: AB=EC
AB=CD
Do đó: EC=CD
mà C,E,D thẳng hàng
nên C là trung điểm của DE