1> Cho SABCD có đáy là hình thoi cạnh a, góc ABC = 60° và tam giác SAC đều vuông góc với đáy tính V =? 2> cho SABCD có đáy là hình chữ nhật với AD = 2AB, tam giác SAB đều và vuông góc với đáy, SC = a√5 tính V =? Mọi người giúp em với ạ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
AH
Akai Haruma
Giáo viên
22 tháng 6 2021
Lời giải:
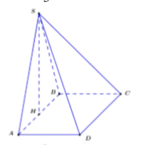
Lấy $H$ là trung điểm $AB$ thì do $SAB$ cân tại $S$ nên $SH\perp BH$
$BH$ là giao tuyến của $(SAB), (ABCD)$; (SAB)\perp (ABCD)$ nên $SH\perp (ABCD)$
$\Rightarrow (SC, (ABCD))=(SC, CH)=\widehat{SCH}=45^0$
$\Rightarrow SH=CH=\sqrt{BC^2+BH^2}=\sqrt{(2a)^2+(\frac{a}{2})^2}=\frac{\sqrt{17}}{2}a$
\(V_{S.ABCD}=\frac{1}{3}.SH.S_{ABCD}=\frac{1}{3}.\frac{\sqrt{17}}{2}a.a.2a=\frac{\sqrt{17}}{3}a^3\)
NV
Nguyễn Việt Lâm
Giáo viên
26 tháng 2 2023
Đề bài thiếu dữ liệu định vị điểm S (ví dụ SC bằng bao nhiêu đó) nên ko thể tính góc giữa SB và (ABCD)
CM
6 tháng 12 2017
Phương pháp:
Công thức tính thể tích khối chóp có diện tích đáy S và chiều cao h là: V = 1 3 S h
Cách giải:
NV
Nguyễn Việt Lâm
Giáo viên
29 tháng 1
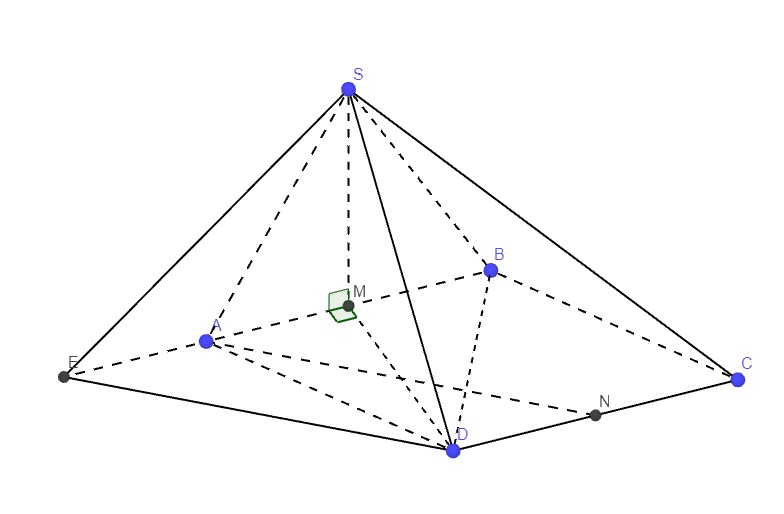
Gọi E là điểm đối xứng M qua A
\(\Rightarrow ANDE\) là hình bình hành (cặp cạnh đối AE và DN song song và bằng nhau)
\(\Rightarrow AN||DE\Rightarrow\) góc giữa AN và SD bằng góc giữa SD và DE
Do tam giác ABD đều \(\Rightarrow MD\perp AB\) \(\Rightarrow\Delta MDE\) vuông tại M
Do tam giác SAB đều \(\Rightarrow SM\perp AB\)
Mà \(\left(SAB\right)\perp\left(ABCD\right)\Rightarrow SM\perp\left(ABCD\right)\)
\(\Rightarrow\) Các tam giác SMD, SME vuông tại M
\(SM=\dfrac{AB\sqrt{3}}{2}=\dfrac{a\sqrt{3}}{2}\) (trung tuyến tam giác SAB đều)
\(MD=\dfrac{AB\sqrt{3}}{2}=\dfrac{a\sqrt{3}}{2}\) (trung tuyến tam giác ABD đều)
\(ME=2AM=AB=a\)
Pitago:
\(SD=\sqrt{SM^2+MD^2}=\dfrac{a\sqrt{6}}{2}\)
\(SE=\sqrt{SM^2+ME^2}=\dfrac{a\sqrt{7}}{2}\)
\(ED=\sqrt{MD^2+ME^2}=\dfrac{a\sqrt{7}}{2}\)
\(\Rightarrow cos\widehat{SDE}=\dfrac{SD^2+ED^2-SE^2}{2SD.ED}=\dfrac{\sqrt{42}}{14}\)
1.
\(\widehat{ABC}=60^0\Rightarrow\Delta ABC\) đều
\(\Rightarrow S_{ABCD}=2S_{ABC}=2.\dfrac{a^2\sqrt{3}}{4}=\dfrac{a^2\sqrt{3}}{2}\)
Gọi O là giao điểm 2 đường chéo \(\Rightarrow SO\perp AC\Rightarrow SO\perp\left(ABCD\right)\)
\(SO=\dfrac{AC\sqrt{3}}{2}=\dfrac{a\sqrt{3}}{2}\) (trung tuyến tam giác đều)
\(V=\dfrac{1}{3}SO.S_{ABCD}=\dfrac{a^3}{4}\)
2.
Gọi M là trung điểm AB \(\Rightarrow SM\perp AB\Rightarrow SM\perp\left(ABCD\right)\)
\(SM=\dfrac{AB\sqrt{3}}{2}\) (trung tuyến tam giác đều)
Áp dụng định lý Pitago cho tam giác vuông MBC:
\(CM^2=BM^2+BC^2=\left(\dfrac{AB}{2}\right)^2+\left(2AB\right)^2=\dfrac{17AB^2}{4}\)
Áp dụng định lý Pitago cho tam giác vuông SMC:
\(SC^2=SM^2+CM^2\Leftrightarrow5a^2=\dfrac{3AB^2}{4}+\dfrac{17AB^2}{4}=5AB^2\)
\(\Rightarrow AB=a\Rightarrow\left\{{}\begin{matrix}AD=2a\\SM=\dfrac{a\sqrt{3}}{2}\end{matrix}\right.\)
\(V=\dfrac{1}{3}.SM.AB.AD=\dfrac{a^3\sqrt{3}}{3}\)