Cho hình vuông ABCD cạnh a túng các tích vô hướng a. Vectơ AB.AC b. vectơ AC.BD
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
22 tháng 12 2022
\(\overrightarrow{AB}.\overrightarrow{CD}=\overrightarrow{AB}\left(\overrightarrow{CB}+\overrightarrow{BA}+\overrightarrow{AD}\right)\)
\(=\overrightarrow{AB}.\overrightarrow{CB}+\overrightarrow{AB}.\overrightarrow{BA}+\overrightarrow{AB}.\overrightarrow{AD}\)
\(=0-\overrightarrow{AB}^2+0=-4a^2\)
HQ
Hà Quang Minh
Giáo viên
25 tháng 9 2023
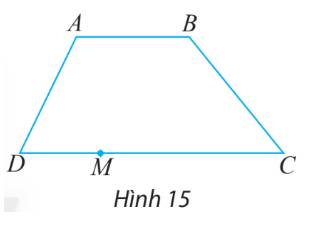
a) ABCD là hình thang nên AB//CD
Các vectơ cùng hướng với vectơ \(\overrightarrow {AB} \) là các vectơ có hướng từ trái qua phải nên đó là: \(\overrightarrow {DC} ,\overrightarrow {DM} ,\overrightarrow {MC} \)
b) \(\overrightarrow {DM} \)có hướng từ trái sang phải nên các vectơ ngược hướng với vectơ \(\overrightarrow {DM} \)là \(\overrightarrow {BA} ,\overrightarrow {MD} ,\overrightarrow {CM} ,\overrightarrow {CD} \)
CM
6 tháng 1 2019
a → . b → = a → . b → . cos a → , b → = 8.10. cos 30 ° = 80. 3 2 = 40 3
CHỌN C
CM
7 tháng 7 2019
a → . b → = a → . b → . cos a → , b → = 4.6. cos 120 ° = 24. − 1 2 = − 12
CHỌN B.
HQ
Hà Quang Minh
Giáo viên
25 tháng 9 2023
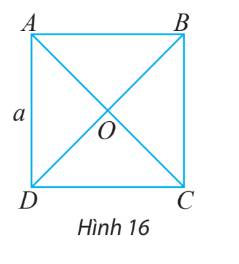
a) \(AC = BD = \sqrt {A{D^2} + D{C^2}} = \sqrt {{a^2} + {a^2}} = a\sqrt 2 \)
\( \Rightarrow AO = OC = BO = OD = \frac{{a\sqrt 2 }}{2}\)
Suy ra các cặp vectơ bằng nhau và có độ dài bằng \(\frac{{a\sqrt 2 }}{2}\) là:
\(\overrightarrow {AO} \)và \(\overrightarrow {OC} \); \(\overrightarrow {CO} \) và \(\overrightarrow {OA} \); \(\overrightarrow {DO} \) và \(\overrightarrow {OB} \); \(\overrightarrow {OD} \) và \(\overrightarrow {BO} \)
b) Trong hình chỉ có 2 đoạn thẳng AC và BD có độ dài là \(a\sqrt 2\).
Do đó hai vectơ đối nhau và có độ dài bằng \(a\sqrt 2\) là:
\(\overrightarrow {AC} \)và \(\overrightarrow {CA} \); \(\overrightarrow {BD} \) và \(\overrightarrow {DB} \).
a: ABCD là hình vuông
=>AC là phân giác của góc BAD và \(AC^2=AB^2+BC^2\)
AC là phân giác của góc BAD
=>\(\widehat{BAC}=\widehat{DAC}=\dfrac{1}{2}\cdot90^0=45^0\)
\(AC^2=AB^2+BC^2\)
=>\(AC^2=a^2+a^2=2a^2\)
=>\(AC=a\sqrt{2}\)
\(\overrightarrow{AB}\cdot\overrightarrow{AC}=AB\cdot AC\cdot cos\left(\overrightarrow{AB};\overrightarrow{AC}\right)\)
\(=a\cdot a\sqrt{2}\cdot cosBAC\)
\(=a^2\cdot\sqrt{2}\cdot\dfrac{\sqrt{2}}{2}=a^2\)
b: Vì ABCD là hình vuông
nên AC\(\perp\)BD
=>\(\overrightarrow{AC}\cdot\overrightarrow{BD}=0\)