Chứng minh công thức tổng quát tương đương vơi công thức truy hồi trong dãy tuyến tính truy hồi cấp hai khi phương trình đặc trưng có hai nghiệm.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đáp án C
Cấp số nhân có công thức truy hồi dạng u 1 = a u n + 1 = q . u n
Dãy số u 1 = - 1 u n + 1 = 3 u n là CSN với u 1 = - 1 và công sai q = 3.

Đặt \(\dfrac{u_n}{n+1}=v_n\)
\(GT\Rightarrow\left\{{}\begin{matrix}v_1=\dfrac{u_1}{1+1}=1\\v_{n+1}=\dfrac{1}{4}v_n,\forall n\in N\text{*}\end{matrix}\right.\)
\(\Rightarrow v_n=\dfrac{1}{4}^{n-1},\forall n\in N\text{*}\)
\(\Rightarrow u_n=\left(n+1\right).\dfrac{1}{4}^{n-1},\forall n\in N\text{*}\)

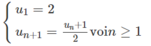
Ta có
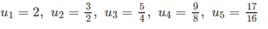
Dự đoán

Chứng minh dự đoán trên bằng quy nạp (bạn đọc tự chứng minh).
Từ đó
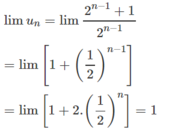

a) \({u_1} = 1\)
\( \Rightarrow {u_2} = 2.1 = 2\)
\( \Rightarrow {u_3} = 3.2 = 6\)
\( \Rightarrow {u_4} = 4.6 = 24\)
\( \Rightarrow {u_5} = 5.24 = 120\)
b)
Ta có:
\({u_2} = 2 = 2.1 \)
\({u_3} = 6= 1.2.3 \)
\({u_4} = 24 = 1.2.3.4\)
\({u_5} = 120 = 1.2.3.4.5\)
\( \Rightarrow {u_n} = 1.2.3....n = n!\).

un+1 = 1+ (n+4).3n+1 = 1 + (n+3).3n+1 + 3n+1
= 1 + 3n.(n+3).3 + 3n+1 = 3[1 + (n+ 3).3n] + 3n+1 – 2 = 3un + 3n+1 -2
Đáp án là D
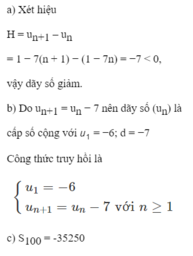
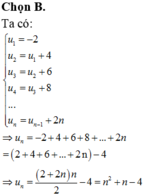

Gọi 1/4 số a là 0,25 . Ta có :
a . 3 - a . 0,25 = 147,07
a . (3 - 0,25) = 147,07 ( 1 số nhân 1 hiệu )
a . 2,75 = 147,07
a = 147,07 : 2,75
a = 53,48
Ta có:
\(U_{n+2}=\alpha\lambda_1^{n+2}+\beta\lambda_2^{n+2}=\alpha\lambda_1^{n+1}.\lambda_1+\beta\lambda_2^{n+1}.\lambda_2\)
\(\Leftrightarrow U_{n+2}=\left(\alpha\lambda_1^{n+1}+\beta\lambda_2^{n+1}\right)\left(\lambda_1+\lambda_2\right)-\alpha\lambda_1^{n+1}.\lambda_2+\beta\lambda_2^{n+1}.\lambda_1\)
\(\Leftrightarrow U_{n+2}=\left(a\lambda_1^{n+1}+\beta\lambda_2^{n+1}\right)\left(\lambda_1+\lambda_2\right)-\lambda_1\lambda_2.\left(\alpha\lambda_1^n+\beta\lambda_2^n\right)\)
\(\Leftrightarrow U_{n+2}=U_{n+1}.\left(\lambda_1+\lambda_2\right)-U_n.\lambda_1\lambda_2\)
Ta lại có \(\lambda_1,\lambda_2\) là nghiệm của phương trình đặc trưng \(a\lambda^2+b\lambda+c=0\)
\(\Rightarrow U_{n+2}=U_{n+1}.\left(\lambda_1+\lambda_2\right)-U_n.\lambda_1\lambda_2=U_{n+1}.\frac{-b}{a}-U_n.\frac{c}{a}\)
\(\Leftrightarrow aU_{n+2}+bU_{n+1}+cU_n=0\left(dpcm\right)\)