cho hình bình hành ABCD biết AD=2AB=10cm. Tính độ dài vecto AD + vecto BD
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


AD=2AB=10cm
=>\(AB=\dfrac{10}{2}=5\left(cm\right)\)
ABCD là hình chữ nhật
=>\(DB^2=DA^2+AB^2\)
=>\(DB^2=10^2+5^2=125\)
=>\(DB=\sqrt{125}=5\sqrt{5}\left(cm\right)\)
Gọi K là trung điểm của AB
Xét ΔDAB có DK là đường trung tuyến
nên \(\overrightarrow{DA}+\overrightarrow{DB}=2\cdot\overrightarrow{DK}\)
K là trung điểm của AB
=>\(KA=\dfrac{5}{2}=2,5\left(cm\right)\)
ΔKAD vuông tại A
=>\(DK^2=DA^2+AK^2\)
=>\(DK^2=10^2+2,5^2=106,25\)
=>\(DK=\dfrac{5\sqrt{17}}{2}\left(cm\right)\)
\(\left|\overrightarrow{AD}+\overrightarrow{BD}\right|=\left|-\overrightarrow{DA}-\overrightarrow{DB}\right|\)
\(=\left|\overrightarrow{DA}+\overrightarrow{DB}\right|=\left|2\cdot\overrightarrow{DK}\right|\)
\(=2\cdot DK\)
\(=2\cdot\dfrac{5\sqrt{17}}{2}=5\sqrt{17}\)

\(\left|\overrightarrow{AB}+\overrightarrow{BD}\right|=\left|\overrightarrow{AD}\right|\)
\(=AD=10\left(cm\right)\)

Sai thì thôi nha :>
Theo đề ra: ABCD là hình bình hành
\(vectoAD+vectoAB=vectoAC\) và \(vectoAB+vectoAC=vectoBD\)
\(\Leftrightarrow vectoAD=-vectoAB+vectoAC\)
\(\Leftrightarrow vectoAD=vectoAB+vectoAC-2vectoAB=vectoBD-2vectoAB=b-2a\)
\(\overrightarrow{BD}=\overrightarrow{BA}+\overrightarrow{BC}=-\overrightarrow{AB}+\overrightarrow{AD}\)
\(\overrightarrow{AC}=\overrightarrow{AB}+\overrightarrow{AD}\)
suy ra \(2\overrightarrow{AD}=\overrightarrow{BD}+\overrightarrow{AC}\Leftrightarrow\overrightarrow{AD}=\frac{\overrightarrow{BD}+\overrightarrow{AC}}{2}=\frac{a+b}{2}\).

a) Ta có: \(\left\{ \begin{array}{l}AD//BC\\AD = BC\end{array} \right.\) (do tứ giác ABCD là hình bình hành)
\( \Rightarrow \overrightarrow {AD} = \overrightarrow {BC} \)
b) Ta có: \(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \)

a: \(\overrightarrow{BD}-\overrightarrow{BA}=\overrightarrow{AD}\)
b: \(\overrightarrow{BC}-\overrightarrow{BD}+\overrightarrow{BA}=\overrightarrow{BD}-\overrightarrow{BD}=\overrightarrow{0}\)

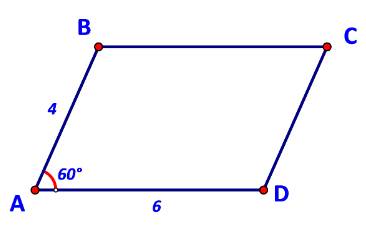
a) \(\overrightarrow {BD} = \overrightarrow {AD} - \overrightarrow {AB} ;\;\overrightarrow {AC} = \overrightarrow {AB} + \overrightarrow {AD} .\)
b) \(\overrightarrow {AB} .\overrightarrow {AD} = 4.6.\cos \widehat {BAD} = 24.\cos {60^o} = 12.\)
\(\begin{array}{l}\overrightarrow {AB} .\overrightarrow {AC} = \overrightarrow {AB} (\overrightarrow {AB} + \overrightarrow {AD} ) = {\overrightarrow {AB} ^2} + \overrightarrow {AB} .\overrightarrow {AD} = {4^2} + 12 = 28.\\\overrightarrow {BD} .\overrightarrow {AC} = (\overrightarrow {AD} - \overrightarrow {AB} )(\overrightarrow {AB} + \overrightarrow {AD} ) = {\overrightarrow {AD} ^2} - {\overrightarrow {AB} ^2} = {6^2} - {4^2} = 20.\end{array}\)
c) Áp dụng định lí cosin cho tam giác ABD ta có:
\(\begin{array}{l}\quad \;B{D^2} = A{B^2} + A{D^2} - 2.AB.AD.\cos A\\ \Leftrightarrow B{D^2} = {4^2} + {6^2} - 2.4.6.\cos {60^o} = 28\\ \Leftrightarrow BD = 2\sqrt 7 .\end{array}\)
Áp dụng định lí cosin cho tam giác ABC ta có:
\(\begin{array}{l}\quad \;A{C^2} = A{B^2} + B{C^2} - 2.AB.BC.\cos B\\ \Leftrightarrow A{C^2} = {4^2} + {6^2} - 2.4.6.\cos {120^o} = 76\\ \Leftrightarrow AC = 2\sqrt {19} .\end{array}\)