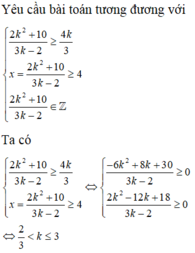tìm nghiệm nguyên của phương trình : \(8x^2+23y^2+16x-44y+16xy-1180=0\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PT
0
LM
2
28 tháng 10 2018
Coi phương trình đã cho là phương trình bậc hai a ẩn x, y là tham số. Dùng điều kiện có nghiệm cuả phương trình để giải
10 tháng 8 2020
pt <=> \(16x^2+32xy+46y^2+32x-88y=2360\)
<=> \(\left(4x+4y+4\right)^2+30y^2-120y+120=2496\)
<=> \(\left(4x+4y+4\right)^2+30\left(y^2-4y+4\right)=2496\)
<=> \(8\left(x+y+1\right)^2+15\left(y-2\right)^2=2496\)
Có: \(15\left(y-2\right)^2\)là 15 lần của 1 SCP
=> \(0\le\left(y-2\right)^2\le\frac{2496}{15}\)
Mà \(\left(y-2\right)^2\)là 1 SCP
=> \(\left(y-2\right)^2=0^2;1^2;...;12^2\)
Đến đây bạn xét từng trường hợp là ra rùi !!!!!!
DG
0
NT
0
16 tháng 12 2021
anh ơi, vậy là sai đề hả anh, chứ đề kêu chứng minh phương trình vô nghiệm mà em thấy anh ghi x=2
NS
0
CM
16 tháng 10 2019
Đáp án D
P T ⇔ π 4 3 x − 9 x 2 − 16 x − 80 = k π ⇔ 3 x − 9 x 2 − 16 x − 80 = 4 k ⇔ 9 x 2 − 16 x − 80 = 3 x − 4 k ⇔ 3 x ≥ 4 k 9 x 2 − 16 x − 80 = 9 x 2 − 24 k x + 16 k 2
Xét 9 x = 18 k 2 + 90 3 k − 2 = 2 9 k 2 − 4 + 98 3 k − 2 = 2 3 k + 2 + 98 3 k − 2
D o x ∈ ℕ * ⇒ 3 k − 2 = 1 ; 2 ; 7 ; 14 ; 49 ; 98 → k ∈ ℤ k = 1 ⇒ x = 12 k = 3 ⇒ x = 4 k = 17 ⇒ x = 12
Chỉ có 2 nghiệm k ; x = 1 ; 12 ; 3 ; 4 thỏa mãn 3 x ≥ 4 k
CM
30 tháng 1 2018
Điều kiện 9 x 2 - 16 x - 80 ≥ 0 ⇔ x ≥ 4
Phương trình đã cho tương đương với
π 4 3 x - 9 x 2 - 16 x - 80 = k π k ∈ ℤ ⇔ 3 x - 9 x 2 - 16 x - 80 = 4 k ⇔ 9 x 2 - 16 x - 80 = 3 x - 4 k ⇔ x ≥ 4 k 3 9 x 2 - 16 x - 80 = 3 x - 4 k 2 ⇔ x ≥ 4 k 3 x = 2 k 2 + 10 3 k - 2
Yêu cầu bài toán tương đương với
2 k 2 + 10 3 k - 2 ≥ 4 k 3 x = 2 k 2 + 10 3 k - 2 ≥ 4 2 k 2 + 10 3 k - 2 ∈ ℤ
Ta có
2 k 2 + 10 3 k - 2 ≥ 4 k 3 x = 2 k 2 + 10 3 k - 2 ≥ 4 ⇔ - 6 k 2 + 8 k + 30 3 k - 2 ≥ 0 2 k 2 - 12 k + 18 3 k - 2 ≥ 0 ⇔ 2 3 < k ≤ 3
Vì k ∈ ℤ nên k ∈ 1 ; 2 ; 3
Với k = 1 suy ra 2 k 2 + 10 3 k - 2 = 12 ∈ Z
Với k = 2 suy ra 2 k 2 + 10 3 k - 2 = 9 2 ∉ 9 2
Với k = 3 suy ra 2 k 2 + 10 3 k - 2 = 4 ∈ Z
Kết hợp với điều kiện ta suy ra x = 4; x = 12
Vậy có 2 giá trị nguyên dương cần tìm
Đáp án C
