: Cho tứ diện SABC. Gọi K,N trung điểm SA và BC. M là điểm thuộc đoạn SC sao cho 3SM = 2MC. Tìm thiết diện của hình chóp và mặt phẳng (KMN)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



+ Trong mp(SAC) gọi giao điểm của AC và KM là E
Trong mp(ABC) gọi I là giao điểm của AB và EN.
Từ đó suy ra thiết diện cần tìm là tứ giác MNIK.
+Trong mp(SAC) dựng AF// SC


a) Ta có:
- M là trung điểm của AB, nên M là trung điểm của đoạn thẳng AB.
- P là trung điểm của SC, nên P là trung điểm của đoạn thẳng SC.
- I là trung điểm của SB, nên I là trung điểm của đoạn thẳng SB.
Vì M, P, I lần lượt là trung điểm của các đoạn thẳng AB, SC, SB, nên ta có:
2AM = AB, 2CP = CS, 2BI = BS.
Giả sử BC không song song với MP. Khi đó, ta có:
- MP cắt BC tại H.
- MP cắt SA tại K.
- MP cắt QN tại L.
Theo định lý , ta có:
AH/HC = AK/KS = AL/LQ.
Từ đó, ta có:
2AM/2CP = AK/KS = AL/LQ.
Tuy nhiên, ta đã biết rằng 2AM/2CP = AB/CS = BS/CS = BI/CS = 2BI/2CP.
Vậy ta có:
2BI/2CP = AK/KS = AL/LQ.
Do đó, ta có AK = AL và KS = LQ.
Từ đó, ta suy ra K = L và Sẽ có MP song song với BC.
Vậy BC // (IMP).
b) Thiết diện của mặt phẳng (α) với hình chóp là một hình tam giác. Để xác định hình tam giác này, cần biết thêm thông tin về góc giữa mặt phẳng (α) và mặt phẳng đáy ABC.
c) Đường thẳng CN và mặt phẳng (SMQ) giao nhau tại một điểm. Để tìm giao điểm này, cần biết thêm thông tin về góc giữa đường thẳng CN và mặt phẳng (SMQ).
--thodagbun--
(Bn tham khảo cách lm đy nhe )

a/
Ta có
\(S\in\left(SAC\right);S\in\left(SBD\right)\)
Trong mp (ABCD) gọi O là giao của AC và BD
\(O\in AC\Rightarrow O\in\left(SAC\right);O\in BD\Rightarrow O\in\left(SBD\right)\)
\(\Rightarrow SO\in\left(SAC\right)\) và \(SO\in\left(SBD\right)\) => SO là giao tuyến của (SAC) và (SBD)
b/
Trong mp (ABCD) Từ G dựng đường thẳng // AC cắt BC tại K
Xét tg SAC có
SM=AM (gt); SN=CN (gt) => MN là đường trung bình của tg SAC
=> MN//AC
Mà GM//AC
=> MN//GK mà \(G\in\left(GMN\right)\Rightarrow GK\in\left(GMN\right)\) (Từ 1 điểm trong mặt phẳng chỉ dựng được duy nhất 1 đường thẳng thuộc mặt phẳng đó và // với 1 đường thẳng cho trươc thuộc mặt phẳng)
\(\Rightarrow K\in\left(GMN\right);K\in BC\) => K llaf giao của BC với (GMN)
c/
Ta có
\(KN\in\left(GMN\right);KN\in\left(SBC\right)\) => KN là giao tuyến của (GMN) với (SBC)
Trong (ABCD) KG cắt AB tại H
\(KG\in\left(GMN\right)\Rightarrow KH\in\left(GMN\right)\)
\(KG\in\left(ABCD\right)\Rightarrow KH\in\left(ABCD\right)\)
=> KH là giao tuyến của (GMN) với (ABCD)
Ta có
\(HM\in\left(SAB\right);HM\in\left(GMN\right)\) => HM là giao tuyến của (GMN) với (SAB)
Trong mp(SAC) gọi P là giao của SO với MN
\(P\in MN\Rightarrow P\in\left(GMN\right)\)
Trong mp(SBD) Nối G với P cắt SD tại Q
\(\Rightarrow GP\in\left(GMN\right)\Rightarrow Q\in GMN\)
\(\Rightarrow MQ\in\left(GMN\right)\) mà \(MQ\in\left(SAD\right)\) => MQ là giao tuyến của (GMN) với (SAD)
Ta có
\(NQ\in\left(GMN\right);NQ\in\left(SCD\right)\) => NQ là giao tuyến của (GMN) với (SCD)
=> thiết diện của hình chóp bị cắt bởi (GMN) là đa giác HMQNK

Đáp án C.


+ (ABD) và (IMK) có điểm chung là k và lần lượt chứa hai đường thẳng AB // MI
=>Giao tuyến của (ABD) và (IMK) là đường thẳng đi qua K và song song với AB và AD tại E =>Thiết diện cần tìm là tứ giác MKEI có M I / / K E M I > K E (1)
+ Δ B M K = Δ A I E ⇒ I E = M K (2)
Từ (1) và (2) =>Tứ giác MKEI là hình thang cân với đáy lớn là MI
+ Có E K = 1 3 ; A B = a 3 ; M I = a 2
Gọi H là hình chiếu vuông góc của E lên MI =>2IH + EK = IM => I H = a 12
I E = A I 2 + A E 2 − 2 A I . A E . c o s 60 ° = a 13 6 ⇒ E H = 13 a 2 36 − a 2 144 = a 51 12
S I M K E = 1 2 E K + I M . E H = 5 a 2 51 144

Đáp án C.
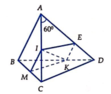
+ (ABD) và (IMK) có điểm chung là k và lần lượt chứa hai đường thẳng AB // MI
=> Giao tuyến của (ABD) và (IMK) là đường thẳng đi qua K và song song với AB và AD tại E Thiết diện cần tìm là tứ giác MKEI có
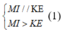
![]()
Từ (1) và (2) => Tứ giác MKEI là hình thang cân với đáy lớn là MI

+ Có
![]()
![]()
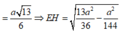
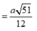
![]()
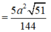
Gọi H là hình chiếu vuông góc của E lên MI 2IH + EK = IM


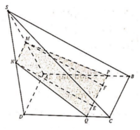
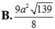
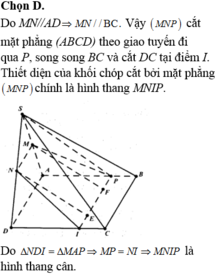

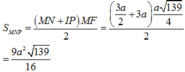
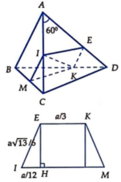


(SAC) có: \(KM\cap AC=I\)
(ABC) có: \(IN\cap AB=J\)
Ta được thiết diện của hình chóp và (KMN) là tứ giác KJNM.