Cứu t đi mn
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Lời giải:
$x^2+2xy+6x+6y+2y^2+8=0$
$\Leftrightarrow (x^2+2xy+y^2)+6x+6y+y^2+8=0$
$\Leftrightarrow (x+y)^2+6(x+y)+y^2+8=0$
$\Leftrightarrow (x+y+3)^2+y^2-1=0$
$\Leftrightarrow (x+y+3)^2=1-y^2\leq 1$
$\Rightarrow -1\leq x+y+3\leq 1$
$\Rightarrow -4\leq x+y\leq -2$
$\Rightarrow 2020\leq x+y+2024\leq 2022$
Vậy $P_{\min}=2020; P_{\max}=2022$


Câu 9:
Các dấu phảy trong câu sau có tác dụng ngăn cách bộ phận cùng làm vị ngữ và ngăn cách các vế trong câu ghép.
Câu 10:
Bằng cách lặp từ ngữ không gian

a: Xét ΔABE và ΔHBE có
BA=BH
\(\widehat{ABE}=\widehat{HBE}\)
BE chung
Do đó: ΔABE=ΔHBE
b: Ta có: ΔABE=ΔHBE
nên BA=BH và EA=EH
=>BE là đường trung trực của AH
d: ta có: EA=EH
mà EH<EC
nên EA<EC

a: Xét (O) có
ΔBEC nội tiếp
BC là đường kính
Do đó: ΔBEC vuông tại E
=>BE\(\perp\)EC tại E
=>BE\(\perp\)AC tại E
b: Xét ΔBFC có
O là trung điểm của BC
OH//CF
Do đó: H là trung điểm của BF

Nghiên cứu khoa học là nghiên cứu dựa vào việc ứng dụng các phương pháp khoa học, khai thác trí tò mò.
Giải thích các bước giải:
Hình thức nghiên cứu này cung cấp thông tin và lý thuyết khoa học nhằm giải thích bản chất và tính chất của thế giới. Nó có thể giúp tạo ra những ứng dụng thực tiễn. Hoạt động nghiên cứu khoa học được tài trợ bởi các cơ quan chính quyền, các tổ chức tài trợ, và các nhóm tư nhân, bao gồm nhiều công ty. Hoạt động nghiên cứu khoa học có thể được phân loại tùy theo lĩnh vực học thuật và ứng dụng. Nghiên cứu khoa học là một tiêu chí được sử dụng rộng rãi trong đánh giá vị thế của một cơ sở học thuật
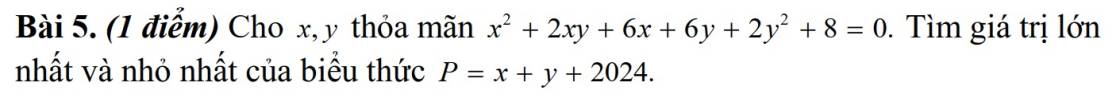 cứu t mn, nhanh nha sáng mai tui đi học rùi chậm nhất là 12h
cứu t mn, nhanh nha sáng mai tui đi học rùi chậm nhất là 12h




a: Trong mp(SBC), gọi M là giao điểm của SO với BC
Chọn mp(SBC) có chứa SO
\(SO\subset\left(SBC\right);SO\subset\left(SAO\right)\)
Do đó: (SBC) giao (SAO)=SO
Vì M là giao điểm của CB với SO
nên M là giao điểm của CB với mp(SAO)
b: Gọi N là giao điểm của AC và BD
\(N\in AC\subset\left(SAC\right)\)
\(N\in BD\subset\left(SBD\right)\)
Do đó: \(N\in\left(SAC\right)\cap\left(SBD\right)\)
mà \(S\in\left(SAC\right)\cap\left(SBD\right)\)
nên (SAC) giao (SBD)=SN
c: Xét (SAB) và (SCD) có
\(S\in\left(SAB\right)\cap\left(SCD\right)\)
AB//CD
Do đó: (SAB) giao (SCD)=xy, xy đi qua S và xy//AB//CD
d: AB//CD
CD\(\subset\)(SCD)
AB không nằm trong mp(SCD)
Do đó: AB//(SCD)