Cho hình chóp SABCD có đáy là hình thang (AB//CD). Gọi M là trung điểm của SD.
a. Xác định giao điểm của SD và MA.
b. Gọi M là trung điểm của SC.
Chứng minh: MN//CD
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HT
22 tháng 12 2020
Đề bài sai òi :v Vẽ hình ra đi bạn.
Giờ tui gán MN vô (SBD) thì giao tuyến của (SBD) và (SBC) là SB. Vậy nên SB phải song song với MN. Nhưng ko :) Song song chết liền hà :)
QT
Quoc Tran Anh Le
Giáo viên
22 tháng 9 2023
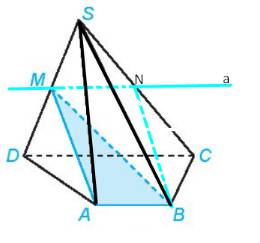
a) mp(MAB) và (SCD)có điểm M chung và chứa hai đường thẳng thẳng song song là AB và CD
Do đó giao tuyến của hai mặt phẳng (MAB) và (SCD) là đường thẳng a đi qua M và song song với CD, AB.
b, Do MN //CD và M là trung điểm của SD.
Suy ra, MN là đường trung bình của tam giác SCD.
3 tháng 1 2021
a) Do MN\(\subset\) (BMN); AD \(\subset\)(ABCD) nên I là một điểm chung của (BMN) với (ABCD). Dễ thấy B là một điểm chung khác I
Vậy (BMN)\(\cap\) (ABCD) =BI
b) J\(\in\)BI\(\subset\) (BMN)
J \(\in\) (CD) \(\subset\) (SCD)
nên J là một điểm chung của (BMN) \(\cap\) (SCD)
vậy (SCD) \(\cap\) (BMN) =NJ
Thiết diện của (BMN) với hình chóp là tứ giác AMNJ
c) Áp dụng định lí Menelaus Trong \(\Delta SAD\) có cát tuyến MNI có:
\(\dfrac{ID}{IA}.\dfrac{MA}{MS}.\dfrac{NS}{ND}=1\)
\(\dfrac{ID}{IA}.1.2=1\) => \(\dfrac{ID}{IA}=\dfrac{1}{2}\)
=> D là trung điểm AI
+ Xét tam giác SAI có 2 trung tuyến MI, SD giao nhau tại N => N là trong tâm tam giác SAI
=> \(\dfrac{NI}{MI}=\dfrac{2}{3}\)
Ta có AD//BC
=> \(\dfrac{IK}{BK}=\dfrac{AI}{BC}=\dfrac{2AD}{BC}=2\)(do AD=BC)
=> \(\dfrac{IK}{IB}=\dfrac{2}{3}\)
Xét tam giác MIB có: \(\dfrac{NI}{MI}=\dfrac{IK}{IB}=\dfrac{2}{3}\)
=> BM//NK
NV
Nguyễn Việt Lâm
Giáo viên
27 tháng 12 2020
Trong tam giác SBD, MN là đường trung bình \(\Rightarrow MN||BD\)
\(\Rightarrow MN||\left(ABCD\right)\)
Trong mp (ABCD), qua E kẻ đường thẳng song song BD cắt BC tại F và cắt AD kéo dài tại G
Trong mp (SAD), nối GN kéo dài cắt SA tại P
Ngũ giác PNEFM là thiết diện của (MNE) và chóp
NV
Nguyễn Việt Lâm
Giáo viên
2 tháng 1
Do M là trung điểm SD, N là trung điểm SC \(\Rightarrow MN\) là đường trung bình tam giác SCD
\(\Rightarrow MN||CD\) (1)
Tương tự PQ là đường trung bình tam giác SAB \(\Rightarrow PQ||AB\)
\(\Rightarrow MN||PQ\Rightarrow\) 4 điểm M, N, P, Q đồng phẳng
Lại có MQ là đường trung bình tam giác SAD \(\Rightarrow MQ||AD\)
Mà \(AD\in\left(ABCD\right)\Rightarrow MQ||\left(ABCD\right)\)
Do \(CD\in\left(ABCD\right)\), từ \(\left(1\right)\Rightarrow MN||\left(ABCD\right)\)
Mà \(\left\{{}\begin{matrix}MN\in\left(MNPQ\right)\\MQ\in\left(MNPQ\right)\\MN\cap MQ=M\end{matrix}\right.\)\(\Rightarrow\left(MNPQ\right)||\left(ABCD\right)\)
a: \(M\in SD\)
\(M\in MA\)
Do đó: \(SD\cap MA=\left\{M\right\}\)
b: Sửa đề: N là trung điểm của SC
Xét ΔSCD có
M,N lần lượt là trung điểm của SD,SC
=>MN là đường trung bình của ΔSCD
=>MN//CD