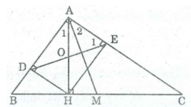
Cho tam giác ABC vuông tại A, đường cao AH. Gọi D, E theo thứ tự là chân đường
vuông góc kẻ từ H đến AB, AC. Gọi M là trung điểm của BC. Chứng minh AM vuông góc với DE.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét tứ giác ADHE có
\(\widehat{ADH}=\widehat{AEH}=\widehat{DAE}=90^0\)
=>ADHE là hình chữ nhật
=>\(\widehat{AED}=\widehat{AHD}\)
AM\(\perp\)DE
=>\(\widehat{AED}+\widehat{MAC}=90^0\)
mà \(\widehat{AED}=\widehat{AHD}\left(cmt\right)\)
và \(\widehat{AHD}=\widehat{ABH}\left(=90^0-\widehat{HAB}\right)\)
nên \(\widehat{ABH}+\widehat{MAC}=90^0\)
mà \(\widehat{ABH}+\widehat{MCA}=90^0\)(ΔABC vuông tại A)
nên \(\widehat{MAC}=\widehat{MCA}\)
=>MA=MC
\(\widehat{MAC}+\widehat{MAB}=\widehat{BAC}=90^0\)
\(\widehat{MCA}+\widehat{MBA}=90^0\)(ΔABC vuông tại A)
mà \(\widehat{MAC}=\widehat{MCA}\)
nên \(\widehat{MAB}=\widehat{MBA}\)
=>MA=MB
mà MA=MC
nên MB=MC
=>M là trung điểm của BC
( Hình em tự vẽ nhé! )
Lấy O là giao điểm DE và HA
+ Xét tứ giác ADHE có:
\(\widehat{HDA}=\widehat{DAE}=\widehat{AEH}=90^o\)
=> ADHE là hình chữ nhật
=> O là trung điểm AH (t/c)
O là trung điểm DE (t/c)
=> OA = OH = OD = OE
=> ΔAOE cân tại O
=> \(\widehat{OAE}=\widehat{OEA}\left(tc\right)\)
+ Xét ΔABH vuông tại H
=> \(\widehat{BAH}+\widehat{ABH}=90^o\)
Mà \(\widehat{BAH}+\widehat{CAH}=90^o\)
=> \(\widehat{ABH}=\widehat{CAH}\)
Mà \(\widehat{CAH}=\widehat{OEH}\)
\(\widehat{ABH}=\widehat{AEO}\)
+ Xét ΔADE và ΔACB có:
\(\widehat{DAE}=\widehat{CAB}\left(=90^o\right)\)
\(\widehat{AED}=\widehat{ABC}\)
=> ΔADE \(\sim\) ΔACB (g.g)
=> \(\widehat{ADE}=\widehat{ACB}\left(2gtu\right)\)
Lấy I là giao điểm AM và DE
+ Xét ΔAIE vuông tại I
=> \(\widehat{IAE}+\widehat{IEA}=90^o\)
Mà \(\widehat{BAM}+\widehat{MAC}=90^o\)
=> \(\widehat{IEA}=\widehat{MAB}\)
Mà \(\widehat{IEA}=\widehat{ABC}\)
=> \(\widehat{ABC}=\widehat{BAM}\)
=> ΔABM cân tại M
=> MA = MB (t/c)
+ Xét ΔAID vuông tại I
=> \(\widehat{IDA}+\widehat{IAD}=90^o\)
Mà \(\widehat{IAD}+\widehat{MAC}=90^o\)
=> \(\widehat{IDA}=\widehat{MAC}\)
Mà \(\widehat{IDA}=\widehat{ACM}\)
=> \(\widehat{MAC}=\widehat{ACM}\)
=> ΔMAC cân tại M
=> MA = MC (t/c)
Mà MA = MB
=> MB = MC
=> M là trung điểm BC.

1: Xét tứ giác ADHE có
\(\widehat{ADH}=\widehat{AEH}=\widehat{DAE}=90^0\)
=>ADHE là hình chữ nhật
=>AH=DE
2: \(\widehat{EDM}=90^0\)
=>\(\widehat{EDH}+\widehat{MDH}=90^0\)
=>\(\widehat{EAH}+\widehat{MDH}=90^0\)
=>\(\widehat{MDH}+\widehat{HAC}=90^0\)
=>\(\widehat{MDH}+\widehat{ABC}=90^0\)
mà \(\widehat{MHD}+\widehat{MBD}=90^0\)
nên \(\widehat{MDH}=\widehat{MHD}\)
=>MD=MH
\(\widehat{MDH}+\widehat{MDB}=\widehat{HDB}=90^0\)
\(\widehat{MHD}+\widehat{MBD}=90^0\)(ΔHDB vuông tại D)
mà \(\widehat{MDH}=\widehat{MHD}\)
nên \(\widehat{MDB}=\widehat{MBD}\)
=>MD=MB
=>MB=MH
=>M là trung điểm của BH
\(\widehat{NED}=90^0\)
=>\(\widehat{NEH}+\widehat{DEH}=90^0\)
=>\(\widehat{NEH}+\widehat{DAH}=90^0\)
mà \(\widehat{DAH}=\widehat{C}\left(=90^0-\widehat{ABC}\right)\)
nên \(\widehat{NEH}+\widehat{C}=90^0\)
mà \(\widehat{NHE}+\widehat{C}=90^0\)(ΔHEC vuông tại E)
nên \(\widehat{NEH}=\widehat{NHE}\)
=>NE=NH
\(\widehat{NEH}+\widehat{NEC}=\widehat{CEH}=90^0\)
\(\widehat{NHE}+\widehat{NCE}=90^0\)(ΔCEH vuông tại E)
mà \(\widehat{NHE}=\widehat{NEH}\)
nên \(\widehat{NEC}=\widehat{NCE}\)
=>NE=NC
mà NH=NE
nên NC=NH
=>N là trung điểm của HC

a, Vì \(\widehat{AEH}=\widehat{ADH}=\widehat{DAE}=90^0\) nên AEHD là hcn
Do đó AH=DE
b, Vì \(\widehat{HAB}=\widehat{MCA}\) (cùng phụ \(\widehat{CAH}\))
Mà \(\widehat{MCA}=\widehat{MAC}\) (do \(AM=CM=\dfrac{1}{2}BC\) theo tc trung tuyến ứng ch)
Vậy \(\widehat{HAB}=\widehat{MAC}\)
c, Gọi O là giao AM và DE
Vì AEHD là hcn nên \(\widehat{HAB}=\widehat{ADE}\Rightarrow\widehat{MAC}=\widehat{ADE}\)
Mà \(\widehat{ADE}+\widehat{AED}=90^0\left(\Delta AED\perp A\right)\) nên \(\widehat{MAC}+\widehat{ADE}=90^0\)
Xét tam giác AOE có \(\widehat{AOE}=180^0-\left(\widehat{MAC}+\widehat{ADE}\right)=90^0\)
Vậy AM⊥DE tại O

Xét tứ giác ADHE, ta có:
∠ A = 90 0 (gt)
∠ (ADH) = 90 0 (vì HD ⊥ AB)
∠ (AEH) = 90 0 (vì HE ⊥ AC)
Suy ra tứ giác ADHE là hình chữ nhật (vì có 3 góc vuông).
+ Xét ∆ ADH và ∆ EHD có :
DH chung
AD = EH ( vì ADHE là hình chữ nhật)
∠ (ADN) = ∠ (EHD) = 90 0
Suy ra: ∆ ADH = ∆ EHD (c.g.c)
⇒ ∠ A 1 = ∠ (HED)
Lại có: ∠ (HED) + ∠ E 1 = ∠ (HEA) = 90 0
Suy ra: ∠ E 1 + ∠ A 1 = 90 0
∠ A 1 = ∠ A 2 (chứng minh trên) ⇒ ∠ E 1 + ∠ A 2 = 90 0
Gọi I là giao điểm của AM và DE.
Trong ∆ AIE ta có: ∠ (AIE) = 180o – ( ∠ E 1 + ∠ A 2 ) = 180 0 - 90 0 = 90 0
Vậy AM ⊥ DE.

a: Xét tứ giác ADHE có
\(\widehat{ADH}=\widehat{AEH}=\widehat{DAE}=90^0\)
=>ADHE là hình chữ nhật
b: ΔHDB vuông tại D
mà DI là đường trung tuyến
nên \(DI=IH=IB\)
Xét ΔIHD có IH=ID
nên ΔIHD cân tại I
=>\(\widehat{IHD}=\widehat{IDH}\)
mà \(\widehat{IHD}=\widehat{HCA}\)(hai góc đồng vị, HD//AC)
nên \(\widehat{IDH}=\widehat{HCA}\)
ADHE là hình chữ nhật
=>\(\widehat{EAH}=\widehat{EDH}\)
=>\(\widehat{EDH}=\widehat{HAC}\)
\(\widehat{IDE}=\widehat{IDH}+\widehat{EDH}\)
\(=\widehat{HAC}+\widehat{HCA}\)
\(=90^0\)
=>DI\(\)\(\perp\)DE
c: ΔCEH vuông tại E
mà EK là đường trung tuyến
nên EK=KH=KC
Xét ΔKEH có KE=KH
nên ΔKEH cân tại K
=>\(\widehat{KEH}=\widehat{KHE}\)
mà \(\widehat{KHE}=\widehat{CBA}\)(hai góc đồng vị, HE//AB)
nên \(\widehat{KEH}=\widehat{CBA}=\widehat{HBA}\)
ADHE là hình chữ nhật
=>\(\widehat{HAD}=\widehat{HED}\)
=>\(\widehat{HED}=\widehat{HAB}\)
\(\widehat{KED}=\widehat{KEH}+\widehat{DEH}\)
\(=\widehat{HAB}+\widehat{HBA}=90^0\)
=>KE\(\perp\)DE
Ta có: KE\(\perp\)DE
ID\(\perp\)KE
Do đó: ID//KE
Xét tứ giác KEDI có
KE//DI
KE\(\perp\)ED
Do đó: KEDI là hình thang vuông
d: DI=1cm
mà HB=2DI
nên HB=2*1=2=2cm
EK=4cm
mà CH=2EK
nên \(CH=2\cdot4=8cm\)
BC=BH+CH
=2+8
=10cm
Xét ΔABC có AH là đường cao
nên \(S_{ABC}=\dfrac{1}{2}\cdot AH\cdot BC=\dfrac{1}{2}\cdot6\cdot10=30\left(cm^2\right)\)

a: Xét tứ giác ADHE có
\(\widehat{EAD}=\widehat{AEH}=\widehat{ADH}=90^0\)
Do đó: ADHE là hình chữ nhật
Suy ra: AH=DE
Xét tứ giác ADHE có
\(\widehat{ADH}=\widehat{AEH}=\widehat{EAD}=90^0\)
=>ADHE là hình chữ nhật
=>\(\widehat{AED}=\widehat{AHD}\)
mà \(\widehat{AHD}=\widehat{ABC}\left(=90^0-\widehat{HAB}\right)\)
nên \(\widehat{AED}=\widehat{ABC}\)
ΔABC vuông tại A
mà AM là đường trung tuyến
nên MA=MC=MB
MA=MC
=>ΔMAC cân tại M
=>\(\widehat{MAC}=\widehat{MCA}=\widehat{ACB}\)
\(\widehat{MAC}+\widehat{AED}=\widehat{ACB}+\widehat{ABC}=90^0\)
=>AM vuông góc DE