- Chế tạo được mô hình đơn giản minh họa định luật bảo toàn năng lượng.
- Giải thích được nếu một vật chuyển động lên dốc, xuống dốc hoặc trên mặt phẳng ngang thì công của trọng lực đóng vai trò gì.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
VT
9 tháng 4 2018
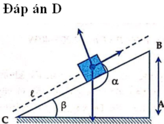
Công của trọng lực thực hiện từ lúc vật lên dốc đến lúc dừng lại trên dốc bằng: Ap=mgh
Với h là hiệu độ cao từ vị trí đầu đến vị trí cuối, tính theo hình ta có:
VT
28 tháng 12 2017
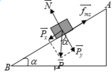
a. Ta có
sin α = 1 2 ; cos α = 3 2
Công của trọng lực
A P = P x . s = P sin α . s = m g sin α . s A P = 2.10. 1 2 .2 = 20 ( J )
Công của lực ma sát
A f m s = − f m s . s = − μ N . s = − μ . m g cos α . s A f m s = − 1 3 .2.10. 3 2 .2 = − 20 ( J )
b. Áp dụng định lý động năng
A = W d B − W d A ⇒ A P → + A f → m s = 1 2 m v B 2 − 1 2 m v A 2 ⇒ 20 − 20 = 1 2 .2 v B 2 − 1 2 .2.2 2 ⇒ v B = 2 ( m / s )
c. Áp dụng định lý động năng
A = W d C − W d B ⇒ A f → m s = 1 2 m v C 2 − 1 2 m v B 2
Công của lực ma sát
A f m s = − f m s . s = − μ N . s = − μ . m g . s / = − μ .2.10.2 = − μ 40 ( J )
Dừng lại
v C = 0 ( m / s ) ⇒ − μ 40 = 0 − 1 2 .2.2 2 ⇒ μ = 0 , 1
VT
27 tháng 6 2017
a. Chọn hệ quy chiếu Oxy như hình vẽ, chiều dương là chiều chuyển động
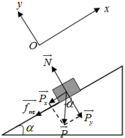
Vật chịu tác dụng của các lực N → ; P → ; f → m s
Theo định luật II newton ta có: N → + P → + f → m s = m a →
Chiếu Ox ta có − P x − f m s = m a
⇒ − P sin α − μ N = m a ( 1 )
Chiếu Oy: N = P y = P cos α ( 2 )
Thay (2) vào (1) ⇒ − P sin α − μ P cos α = m a
⇒ a = − g sin α − μ g cos α
Mà sin α = 30 50 = 3 5 ; cos α = 50 2 − 30 2 50 = 4 5
⇒ a = − 10. 3 5 − 0 , 25.10. 4 5 = − 8 m / s 2
Khi lên tới đỉnh dốc thì v = 0 m / s ta có
v 2 − v 0 2 = 2 a s ⇒ 0 2 − v 0 2 = 2. − 8 .50 ⇒ v 0 = 20 2 m / s
b. Khi lên đỉnh dốc thì vật tụt dốc ta có: Chọn hệ quy chiếu Oxy như hình vẽ, chiều dương là chiều chuyển động
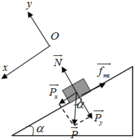
Vật chịu tác dụng của các lực N → ; P → ; f → m s
Theo định luật II newton ta có: N → + P → + f → m s = m a → 1
Chiếu Ox ta có: P x − f m s = m a 1
⇒ P sin α − μ N = m a 1 ( 1 )
Chiếu Oy: N = P y = P cos α ( 2 )
Thay (2) vào (1)
⇒ P sin α − μ P cos α = m a 1 ⇒ a 1 = g sin α − μ g cos α
⇒ a 1 = 10. 3 5 − 0 , 25.10. 4 5 = 4 m / s 2
Áp dụng công thức
v 2 2 − v 2 = 2 a 1 s ⇒ v 2 = 2. a 1 . s = 2.4.0 , 5 = 2 m / s
Thời gian vật lên dốc
v = v 0 + a t 1 ⇒ t 1 = − v 0 a = − 20 2 − 8 = 5 2 2 s
Thời gian xuống dốc
v 2 = v + a 1 t 2 ⇒ t 2 = v 2 a 1 = 2 4 = 0 , 5 s
Thời gian chuyển động kể từ khi bắt đầu lên dốc cho đến khi xuống đến chân dốc : t = t 1 + t 2 = 5 2 2 + 0 , 5 = 4 , 04 s
VT
26 tháng 4 2017
Chọn B
Áp dụng định luật bảo toàn và chuyển hóa cơ năng ở hai vị trí chân dốc và ở vị trí đầu dốc
E 1 − E 0 = μ 1 m g S 1 → S t = 0 1 2 m v 0 2 ⏟ E 0 = 1 2 m v 2 + m g h ⏟ E 1 ⇒ v = v 0 2 − 2 g h
Áp dụng định luật bảo toàn và chuyển hóa cơ năng ở hai vị trí đầu dốc và vị trí vật dừng lại
0 − 1 2 m v 2 = − μ 2 m g . S 2 ⇒ S 2 = v 2 2 μ g = v 0 2 − 2 g h 2 μ g = 4 m
HQ
Hà Quang Minh
Giáo viên
3 tháng 11 2023
a)
Giản đồ vectơ các lực tác dụng lên thùng hàng:
b)
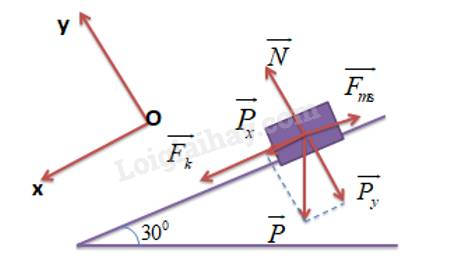
Ta có:
\({P_x} = P.\sin \alpha = 500.\sin {30^0} = 250N\)
\({P_y} = P.\cos \alpha = 500.\cos {30^0} = 500.\frac{{\sqrt 3 }}{2} = 250\sqrt 3 N\)
c)
Lực pháp tuyến của dốc lên thùng hàng không có tác dụng kéo thùng hàng xuống dốc vì nó cân bằng với thành phần \(\overrightarrow {{P_y}} \) của trọng lực.
d)
Chiếu các lực tác dụng lên trục Ox ta được:
\({F_k} - {F_{ms}} = ma \Leftrightarrow {F_k} - \mu N = ma\) (1)
Chiếu các lực tác dụng lên trục Oy ta được:
\(N - P.\cos \alpha = 0 \Leftrightarrow N = P.\cos \alpha = 250\sqrt 3 N\) (2)
Thay vào (1) ta được:
\(250 - \mu .250\sqrt 3 = \frac{{500}}{{10}}.2,00\)
\( \Leftrightarrow \mu = \frac{{150}}{{250\sqrt 3 }} = \frac{{\sqrt 3 }}{5} \approx 0,346\)
Vậy hệ số ma sát trượt giữa mặt dốc và thùng hàng là 0,346.
- Mô hình minh họa định luật bảo toàn năng lượng
Dụng cụ: một viên bi, hai thanh kim loại nhẵn, hai giá đỡ có vít điều chỉnh độ cao.
Chế tạo: Dùng hai thanh kim loại uốn thành đường ray và gắn lên giá đỡ để tạo được mô hình như hình bên.
Thí nghiệm:
+ Thả viên bi từ điểm A trên đường ray.
+ Kiểm chứng xem viên bi có lên được điểm D không?
Kết quả:
+ Viên bi lên gần tới điểm D. Vì:
+ Do trong quá trình viên bi di chuyển từ điểm A trên đường ray, có sự ma sát giữa viên bi và đường ray làm cho cả viên bi và đường ray nóng lên, đồng thời phát ra âm thanh.
+ Năng lượng dự trữ (thế năng trọng trường của viên bi tại điểm A) được chuyển hóa thành động năng để viên bi di chuyển lên gần tới điểm D và một phần năng lượng chuyển hóa thành nhiệt năng và năng lượng âm thanh.
Chứng tỏ năng lượng được bảo toàn, nó chỉ chuyển hóa từ dạng này sang dạng khác.
- Giải thích:
+ Khi một vật chuyển động lên dốc, công của trọng lực là công cản. Vì thành phần \(\overrightarrow{P_x}\) của \(\overrightarrow{P}\) lên phương chuyển động ngược chiều với chiều chuyển động, làm cản trở chuyển động của vật.
+ Khi một vật chuyển động xuống dốc, công của trọng lực là công phát động. Vì thành phần \(\overrightarrow{P_x}\) của \(\overrightarrow{P}\) lên phương chuyển động cùng chiều với chiều chuyển động.
+ Khi một vật chuyển động trên mặt phẳng ngang, trọng lực không thực hiện công. Vì trọng lực vuông góc với phương chuyển động.