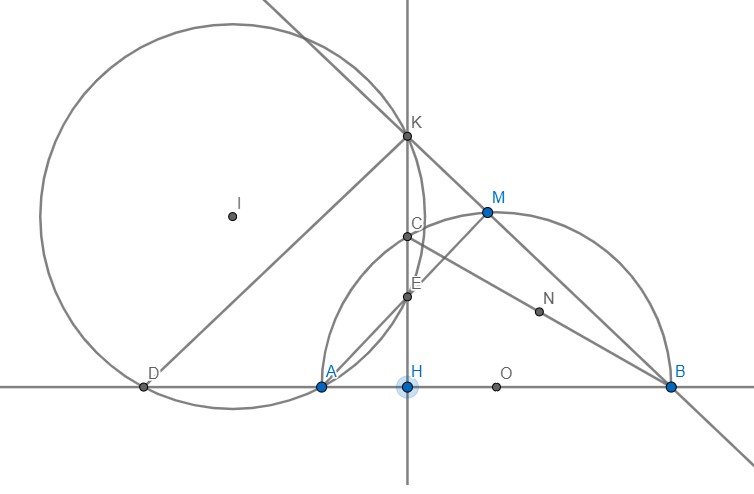
cho nửa đường tròn tâm O đường kính AB. M là điểm bất kì trên cung AB, vẽ MD vuông góc vs AB, trên cung MB lấy C, tiếp tuyến tại C của nửa đường tròn cắt DM tại I;DM cắt AC tại E và cắt BC kéo dài tại F1)CM: tứ giác BCED: ADCF nội tiếp2) CM : góc MEC=góc ABC3) CM: I là tâm đường tròn ngoại tiếp △FECgiúp mik giải bài này vs mik đag cần...
Đọc tiếp
cho nửa đường tròn tâm O đường kính AB. M là điểm bất kì trên cung AB, vẽ MD vuông góc vs AB, trên cung MB lấy C, tiếp tuyến tại C của nửa đường tròn cắt DM tại I;DM cắt AC tại E và cắt BC kéo dài tại F
1)CM: tứ giác BCED: ADCF nội tiếp
2) CM : góc MEC=góc ABC
3) CM: I là tâm đường tròn ngoại tiếp △FEC
giúp mik giải bài này vs 
mik đag cần gấp
1: Xét (O) có
ΔACB nội tiếp
AB là đường kính
Do đó: ΔACB vuông tại C
=>AC\(\perp\)CB tại C
=>AC\(\perp\)BF tại C
Xét tứ giác EDBC có
\(\widehat{EDB}+\widehat{ECB}=90^0+90^0=180^0\)
=>EDBC là tứ giác nội tiếp
Xét tứ giác ADCF có
\(\widehat{ADF}=\widehat{ACF}=90^0\)
=>ADCF là tứ giác nội tiếp
2: EDBC là tứ giác nội tiếp
=>\(\widehat{DEC}+\widehat{DBC}=180^0\)
mà \(\widehat{DEC}+\widehat{IEC}=180^0\)(kề bù)
nên \(\widehat{IEC}=\widehat{DBC}\)
3: \(\widehat{IEC}=\widehat{DBC}=\dfrac{1}{2}\cdot sđ\stackrel\frown{AC}\)(góc DBC là góc nội tiếp chắn cung AC)
\(\widehat{ICE}=\dfrac{1}{2}\cdot sđ\stackrel\frown{CA}\)(góc ICE là góc tạo bởi tiếp tuyến IC và dây cung CA)
Do đó: \(\widehat{IEC}=\widehat{ICE}\)
=>IE=IC
\(\widehat{IEC}+\widehat{IFC}=90^0\)(ΔFCE vuông tại C)
\(\widehat{ICE}+\widehat{ICF}=\widehat{FCE}=90^0\)
mà \(\widehat{IEC}=\widehat{ICE}\)
nên \(\widehat{IFC}=\widehat{ICF}\)
=>IF=IC
mà IC=IE
nên IF=IC=IE
=>I là tâm đường tròn ngoại tiếp ΔCFE
mik c.ơn nhiều