Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Gọi N là trung điểm của SD
Xét ΔSCD có
M,N lần lượt là trung điểm của SC,SD
=>MN là đường trung bình của ΔSCD
=>MN//CD
=>MN//AB
=>N là hình chiếu song song của M theo phương AB lên mp(SAD)
Do (MAB) chứa AB//CD, nên giao tuyến của (MAB) với (SCD) là đường thẳng đi qua M và song song với AB. Đường thẳng này cắt SD tại điểm N. khi đó MN là đường trung bình của tam giác SCD nên N là trung điểm của SD.
Đáp án B
Kéo dài AB và CD cắt nhau tại E
\(\Rightarrow SE=\left(SAB\right)\cap\left(SCD\right)\)
Qua M kẻ đường thẳng d song song CD lần lượt cắt AC và AD tại F và G
Trong mp (SAC), qua F kẻ đường thẳng song song SA cắt SC tại P
Trong mp (SAD), qua G kẻ đường thẳng song song SA cắt SD tại Q
\(\Rightarrow\) Hình thang MPQG là thiết diện của (P) và chóp
Đáp án C
Trong mặt phẳng (ABCD), kẻ DN//CH, dễ thấy AN = AH = HB = SH = a .
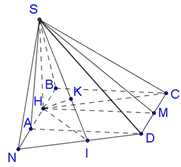
Trong mp (ABCD), nối AN kéo dài cắt BC kéo dài tại E
⇒E∈(SBC)⇒E∈(SBC)
Do AD song song BE, áp dụng Talet:
ANNE=NDNC=1⇒AN=NE⇒ANNE=NDNC=1⇒AN=NE⇒ N là trung điểm AE
⇒MN⇒MN là đường trung bình tam giác SAE
⇒MN//SE⇒MN//(SBC)
Gọi M là trung điểm của SA
Xét ΔSAD có
M,N lần lượt là trung điểm của SA,SD
=>MN là đường trung bình của ΔSAD
=>MN//AD
=>MN//BC
=>M là hình chiếu song song của N theo phương BC lên mp(SAB)