cho tam giác ABC vuông tạ A(AB<AC), D là trung điểm của BC, trên tia đối của tia DA lấy điểm E sao cho DE=DA. Gọi H,K lần lượt làchân đường vuông góc hạ từ B,C xuống đường thẳng AE, M là chân đường vuông góc hạ từ D xuống AC. Chứng Minh CK=BH
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
12 tháng 7 2023
1:
BC=15+20=35cm
AD là phân gíac
=>AB/BD=AC/CD
=>AB/3=AC/4=k
=>AB=3k; AC=4k
AB^2+AC^2=BC^2
=>25k^2=35^2
=>k=7
=>AB=21cm; AC=28cm
AH=21*28/35=16,8cm
\(AD=\dfrac{2\cdot21\cdot28}{21+28}\cdot cos45=12\sqrt{2}\left(cm\right)\)
2:
BC=căn 12^2+16^2=20cm
HB=AB^2/BC=12^2/20=7,2cm
HC=20-7,2=12,8cm
3 tháng 4 2023
a: Xét ΔKBC vuông tại K và ΔHCB vuông tại H có
BC chung
góc KBC=góc HCB
=>ΔKBC=ΔHCB
b: ΔKBC=ΔHCB
=>góc EBC=góc ECB
=>ΔEBC cân tại E
27 tháng 7 2023
a: Xét ΔABD vuông tại A và ΔHBD vuông tại H có
BD chung
góc ABD=góc HBD
=>ΔBAD=ΔBHD
b: Xét ΔDAK vuông tại A và ΔDHC vuông tại H có
DA=DH
góc ADK=góc HDC
=>ΔDAK=ΔDHC
=>DK=DC
=>ΔDKC cân tại D
12 tháng 2 2016
a) tam giác ABC có BC^2=52^2=2704
mà AB^2+AC^2=20^2+48^2=2704
=> BC^2=AB^2+AC^2
=> tam giác ABC vuông tại A
b) tam giác ABC vuông tại A=> AH.BC=AB.AC
=> AH.52=20.48
=> AH.52=960
=> AH=240/13cm
TN
24 tháng 5 2016
trong tgiac vuông tâm đường tròn ngoại tiếp chính là trung điểm cạnh huyền
Áp dụng định lý pytago vào tgiac vuông ABC ta có :
\(BC^2\)=\(AC^2\)+\(AB^2\)
\(BC^2\)=\(8^2\)+\(6^2\)
\(BC^2\)=100
BC=10
Vậy bán kính đường tròn ngoại tiếp tgiac ABC là:
10:2=5cm
NT
24 tháng 5 2016
Gọi bk ngoại tiếp là R còn nôi tiếp là r ;p là 1/2 chu vi (= a+b+c/2)
ra có R=BC/2=5
mà S=pr=(6+8+10)/2r=6*8/2=>r=2
NB
3 tháng 5 2023
a)xét tg ABD và tg CBD có:
+ AB=BE(gt)
+ góc ABD = EBD (BD là phân giác)
+BD chung
=>tg ABD= tg EBD(c.gc)
b) vì tg ABD=tgEBD
=> AD=DE và góc BAD = BED (=90 độ)
=> DE ⊥ BC
=> tg DEC có DC là cạnh huyền =>DC>ED mà ED=AD => DC>AD
c)xét tg BFE và tg BCA có:
+ Góc E = A (=90 độ)
+góc B chung
+ BE=BA
=>tg BFE =tg BCA (gcg)
=>BF=BC
=> tg BFC cân tại B
vì S là td FC
=>BS vừa là trung tuyến vừa là đường cao
=>BS⊥FC (1)
tg BFC có: D là giao của 2 đg cao CA và FE
=> D là trực tâm => BD ⊥ FC (2)
từ 1 và 2 => B,D,S thẳng hàng
KV
3 tháng 5 2023
Sửa đề: AB = BE (không phải AB = AE)
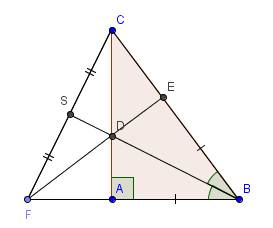
Gởi hình vẽ trước, đi công việc, tí sửa sau
BH\(\perp\)AE
CK\(\perp\)AE
Do đó: BH//CK
Xét ΔDHB vuông tại H và ΔDKC vuông tại K có
DB=DC
\(\widehat{HDB}=\widehat{KDC}\)
Do đó: ΔDHB=ΔDKC
=>HB=KC