tính gía trị lớn nhất của \(\dfrac{5}{x+\sqrt{x}+1}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
10 tháng 3 2023
a: |2x-3|=1
=>2x-3=1 hoặc 2x-3=-1
=>x=1(nhận) hoặc x=2(loại)
KHi x=1 thì \(A=\dfrac{1+1^2}{2-1}=2\)
b: ĐKXĐ: x<>-1; x<>2
\(B=\dfrac{2x^2-4x+3x+3-2x^2-1}{\left(x-2\right)\left(x+1\right)}=\dfrac{-x+2}{\left(x-2\right)\left(x+1\right)}=\dfrac{-1}{x+1}\)
PH
1
27 tháng 1 2022
a, Thay x = 1/4 vào A ta được :
\(A=\dfrac{\dfrac{1}{2}+1}{\dfrac{1}{2}-3}=\dfrac{\dfrac{3}{2}}{-\dfrac{5}{2}}=-\dfrac{3}{5}\)
b, Với x >= 0 ; x khác 1 ; 9
\(B=\dfrac{x+5-3\left(\sqrt{x}+1\right)+\sqrt{x}-1}{x-1}=\dfrac{x-2\sqrt{x}+1}{x-1}=\dfrac{\sqrt{x}-1}{\sqrt{x}+1}\)
HT
Tìm giá trị lớn nhất của
N=\(\dfrac{2x+5}{\sqrt{x}+1}\) khi x≥9
F=\(\dfrac{x+3}{\sqrt{x}+1}\) khi x≥4
2
AH
Akai Haruma
Giáo viên
30 tháng 7 2021
Hai biểu thức này chỉ có min thui bạn nhé.
1.
\(N=\frac{2x+5}{\sqrt{x}+1}=\frac{2\sqrt{x}(\sqrt{x}+1)-2(\sqrt{x}+1)+7}{\sqrt{x}+1}=2\sqrt{x}-2+\frac{7}{\sqrt{x}+1}\)
\(=2(\sqrt{x}+1)+\frac{7}{\sqrt{x}+1}-4\)
\(=\frac{7}{16}(\sqrt{x}+1)+\frac{7}{\sqrt{x}+1}+\frac{25}{16}(\sqrt{x}+1)-4\)
\(\geq 2\sqrt{\frac{7}{16}.7}+\frac{25}{16}(\sqrt{9}+1)-4=\frac{23}{4}\) (theo BĐT AM-GM)
Vậy $N_{\min}=\frac{23}{4}$ khi $x=9$
AH
Akai Haruma
Giáo viên
30 tháng 7 2021
2.
\(F=\frac{x+3}{\sqrt{x}+1}=\frac{\sqrt{x}(\sqrt{x}+1)-(\sqrt{x}+1)+4}{\sqrt{x}+1}=\sqrt{x}-1+\frac{4}{\sqrt{x}+1}\)
\(=\frac{4}{9}(\sqrt{x}+1)+\frac{4}{\sqrt{x}+1}+\frac{5\sqrt{x}}{9}-\frac{13}{9}\)
\(\geq 2\sqrt{\frac{4}{9}.4}+\frac{5\sqrt{4}}{9}-\frac{13}{9}=\frac{7}{3}\)
Vậy $F_{\min}=\frac{7}{3}$ khi $x=4$
12 tháng 8 2021
1 quy đồng lên ra được
2 \(A=\dfrac{1}{x-2\sqrt{x-5}+3}\le\dfrac{1}{5-2.0+3}=\dfrac{1}{8}\)
dấu"=" xảy ra<=>x=5
12 tháng 8 2021
ở câu 1 mình làm cách quy đồng rồi nhưng nó ko ra, bạn có cách khác ko?
27 tháng 2 2021
a) Thay x=4 vào biểu thức \(B=\dfrac{3}{\sqrt{x}-1}\), ta được:
\(B=\dfrac{3}{\sqrt{4}-1}=\dfrac{3}{2-1}=3\)
Vậy: Khi x=4 thì B=3
b) Ta có: P=A-B
\(\Leftrightarrow P=\dfrac{6}{x-1}+\dfrac{\sqrt{x}}{\sqrt{x}+1}-\dfrac{3}{\sqrt{x}-1}\)
\(\Leftrightarrow P=\dfrac{6}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}+\dfrac{\sqrt{x}\left(\sqrt{x}-1\right)}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}-\dfrac{3\left(\sqrt{x}+1\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(\Leftrightarrow P=\dfrac{6+x-\sqrt{x}-3\sqrt{x}-3}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(\Leftrightarrow P=\dfrac{x-\sqrt{x}-3\sqrt{x}+3}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(\Leftrightarrow P=\dfrac{\sqrt{x}\left(\sqrt{x}-1\right)-3\left(\sqrt{x}-1\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(\Leftrightarrow P=\dfrac{\left(\sqrt{x}-1\right)\left(\sqrt{x}-3\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(\Leftrightarrow P=\dfrac{\sqrt{x}-3}{\sqrt{x}+1}\)
AH
Akai Haruma
Giáo viên
31 tháng 12 2023
Lời giải:
$\frac{\sqrt{x}+1}{\sqrt{x}+4}=\frac{\sqrt{x}+4-3}{\sqrt{x}+4}=1-\frac{3}{\sqrt{x}+4}$
Vì $\sqrt{x}\geq 0$ nên $\sqrt{x}+4\geq 4$
$\Rightarrow \frac{3}{\sqrt{x}+4}\leq \frac{3}{4}$
$\Rightarrow \frac{\sqrt{x}+1}{\sqrt{x}+4}=1-\frac{3}{\sqrt{x}+4}\geq 1-\frac{3}{4}=\frac{1}{4}$
Vậy $M=\frac{1}{4}$
------------------
$N=\frac{\sqrt{x}+5}{\sqrt{x}+2}=1+\frac{3}{\sqrt{x}+2}$
Do $\sqrt{x}\geq 0$ nên $\sqrt{x}+2\geq 2$
$\Rightarrow \frac{3}{\sqrt{x}+2}\leq \frac{3}{2}$
$\Rightarrow \frac{\sqrt{x}+5}{\sqrt{x}+2}\leq 1+\frac{3}{2}=\frac{5}{2}$
Vậy $N=\frac{5}{2}$
$\Rightarrow 2M+N =2.\frac{1}{4}+\frac{5}{2}=3$
Đáp án C.
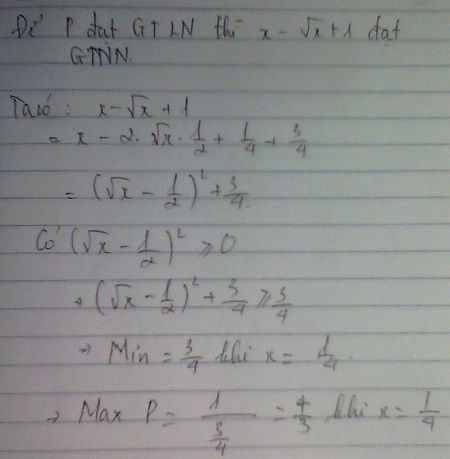
Biểu thức đã cho lớn nhất khi x + √x + 1 nhỏ nhất
ĐKXĐ: x ≥ 0
⇒ x + √x + 1 ≥ 1
⇒ x + √x + 1 nhỏ nhất là 1 khi x = 0
Vậy giá trị lớn nhất của biểu thức đã cho là 5/1 = 5 khi x = 0
Biểu thức đã cho lớn nhất khi x + √x + 1 nhỏ nhất
ĐKXĐ: x ≥ 0
⇒ x + √x + 1 ≥ 1
⇒ x + √x + 1 nhỏ nhất là 1 khi x = 0
Vậy giá trị lớn nhất của biểu thức đã cho là 5/1 = 5 khi x = 0