Cho tam giác abc vuông tại a, đường cao ah, trung tuyến am. Từ h vẽ đường vuông góc với ac, đường thẳng này cắt am tại n. Chứng minh abhn là hình thang cân
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


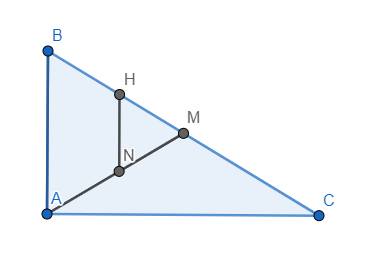
Ta có \(HN\perp AC\) và \(AB\perp AC\) nên AB//HN. Do đó tứ giác ABHN là hình thang (1)
Mặt khác, tam giác ABC vuông tại A có trung tuyến AM nên \(AM=\dfrac{1}{2}BC=BM\), suy ra tam giác MAB cân tại M hay \(\widehat{ABH}=\widehat{NAB}\) (2)
Từ (1) và (2), ta suy ra tứ giác ABHN là hình thang cân. (đpcm)

a) Xét tam giác BEM và tam giácCFM
có:BM=MC(gt)
góc EBM=gócFCM(tam giác ABC can^)
->T/g BEM=t/g CFM(c.huyền g. nhon)
b)
Xét tam giác vg AEM va t/g vg AFM
có:EM=MF(t/g BEM=t/gAFM)
AM là cạnh chung
->t/g AEM =t/g AFM( c/ huyền -c.góc vg)
->AE=AF(2 cạnh tương ứng)
Xét tam giác AEI và t/g AFI
có:MF=EM(t/g BEM= t/g CFM)
AM là cạnh chung
AF=AE(C/ m trên)
->t/g AEI =t/g AFI(c-c-c)
->EI = IF(2 cạnh tương ứng)
->góc AIE= góc AIF(2 tương ứng)
=>AE là đường trung trực của EF
c(mik ko pt lm)
a và b bạn Hương Sơn
c) Ta có:
\(\Delta ABC\)cân
có AM là đường trung tuyến
=> AM cũng là đường trung trực
=> \(AM\perp BC\)
=> AM = 90 độ
Vì \(\Delta ABC\)cân
=> Góc ABM = góc ACM (1)
mà Góc ABD = góc ACD = 90 độ (2)
Từ (1) và (2) => Góc MBD = góc MCD
Xét \(\Delta DMB\)và \(\Delta DMC\)có :
DM : cạnh chung (1)
Góc MBD = góc MCD ( chứng minh trên ) (2)
BM = MC ( vì AM là đường trung tuyến của tam giác ABC ) (3)
Từ (1) ; (2) và (3) => \(\Delta DMB=\Delta DMC\)(cạnh - góc - cạnh)
=> Góc CMD = góc BMD ( cặp góc tương ứng)
Mà Góc CMD + góc BMD = 180 độ
=> Góc CMD = BMD = 180 : 2 = 90 độ
Vì Góc AMC = 90 độ ( vì AM là đường trung trực)
và góc CMD = 90 độ
=> AMC + CMD = AMD
=> 90 + 90 = AMD
=> AMD = 180 độ
=> Ba điểm A ; M ; D thẳng hàng. ( điều phải chứng minh)
Chúc bạn học tốt !

a) Ta có: ΔABH vuông tại H(AH⊥BC)
nên \(\widehat{HAB}+\widehat{ABH}=90^0\)(hai góc nhọn phụ nhau)
hay \(\widehat{HAB}+\widehat{ABM}=90^0\)(1)
Ta có: tia AB nằm giữa hai tia AD,AM(gt)
nên \(\widehat{DAB}+\widehat{MAB}=\widehat{MAD}\)
hay \(\widehat{DAB}+\widehat{MAB}=90^0\)(2)
Ta có: ΔABC vuông tại A(gt)
mà AM là đường trung tuyến ứng với cạnh huyền BC(M là trung điểm của BC)
nên \(AM=\dfrac{BC}{2}\)(Định lí 1 về áp dụng hình chữ nhật vào tam giác vuông)
mà \(BM=\dfrac{BC}{2}\)(M là trung điểm của BC)
nên AM=BM
Xét ΔABM có AM=BM(cmt)
nên ΔABM cân tại M(Định nghĩa tam giác cân)
⇒\(\widehat{MBA}=\widehat{MAB}\)(hai góc ở đáy)(3)
Từ (1), (2) và (3) suy ra \(\widehat{HAB}=\widehat{DAB}\)
mà tia AB nằm giữa hai tia AH,AD
nên AB là tia phân giác của \(\widehat{DAH}\)(đpcm)
làm tương tự
Bài làm
.....................
k mk nhé
hình như đề sai hay sao ấy. đã cho tg ABC vuông cân tại A. đg cao AH r còn có đg trung tuyến AM