Bài 5. Ông Phú gửi tiết kiệm 100 triệu đồng tại một ngân hàng với kì hạn một năm, lãi suất 5% một năm. Hết thời hạn một năm, tiền lãi gộp vào số tiền gửi ban đầu và lại gửi theo thể thức cũ. Cứ như thế sau ba năm thì số tiền cả gốc lẫn lãi là bao nhiêu?
SOS mn ơiiiii

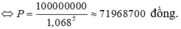
Số tiền cả gốc lẫn lãi sau 1 năm là:
\(100000000\cdot\left(1+5\%\right)=105000000\left(đ\right)\)
Số tiền cả gốc lẫn lãi sau 2 năm tiếp là:
\(105000000\cdot\left(1+5\%\right)=110250000\left(đ\right)\)
Số tiền cả gốc lẫn lãi sau 3 năm tiếp là:
\(110250000\cdot\left(1+5\%\right)=115762500\left(đ\right)\)
Vậy: Cứ như thế sau ba năm thì số tiền cả gốc lẫn lãi là \(115762500\) đồng
(\(100\%=\dfrac{100}{100}=1\)).
Cảm ơn ạ