Cho cấp số nhân thỏa mãn u1+u2+u3=13;u4-u1=26 . Tổng 8 số hạng đầu của cấp số nhân (un) là
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
23 tháng 2 2017
Chọn C
Ta có S 2011 = u 1 q 2011 − 1 q − 1
q = 1 3 ⇒ S 2011 = 243 22 1 − 1 3 2011
q = 3 ⇒ S 2011 = 1 22 3 2011 − 1
CM
11 tháng 5 2018
Chọn C
Gọi q là công bội của cấp số. Khi đó ta có
u 1 + u 2 + u 3 + u 4 + u 5 = 11 u 1 + u 5 = 82 11
⇔ u 2 + u 3 + u 4 = 39 11 u 1 + u 5 = 82 11 ⇔ u 1 q + q 2 + q 3 = 39 11 u 1 1 + q 4 = 82 11
Suy ra:
q 4 + 1 q 3 + q 2 + q = 82 39 ⇔ 39 q 4 − 82 q 3 − 82 q 2 − 82 q + 39 = 0
⇔ ( 3 q − 1 ) ( q − 3 ) ( 13 q 2 + 16 q + 13 ) = 0 ⇔ q = 1 3 , q = 3
q = 1 3 ⇒ u 1 = 81 11 ⇒ u n = 81 11 . 1 3 n − 1
q = 3 ⇒ u 1 = 1 11 ⇒ u n = 3 n − 1 11
U
1
AH
Akai Haruma
Giáo viên
25 tháng 10 2023
Lời giải:
Gọi $q$ là công bội thì $u_2=u_1q; u_3=u_1q^2$.
Theo bài ra ta có:
$24=u_1+u_2+u_3=u_1+u_1q+u_1q^2=u_1(1+q+q^2)(1)$
$364=u_1^2+u_2^2+u_3^2=u_1^2+(u_1q)^2+(u_1q^2)^2$
$=u_1^2(1+q^2+q^4)(2)$
Từ $(1); (2)\Rightarrow \frac{u_1^2(1+q+q^2)^2}{u_1^2(1+q^2+q^4)}=\frac{24^2}{364}$
$\Leftrightarrow \frac{(1+q+q^2)^2}{1+q^2+q^4}=\frac{144}{91}(*)$
Đặt $q=a; q^2+1=b$ thì:
$(*)\Leftrightarrow \frac{(a+b)^2}{b^2-a^2}=\frac{144}{91}$
$\Rightarrow 91(a+b)^2=144(b^2-a^2)$
$\Leftrightarrow (a+b)(235a-53b)=0$
$\Rightarrow a+b=0$ hoặc $235a-53b=0$
Hiển nhiên $a+b=q^2+q+1>0$ nên $235a-53b=0$
$\Leftrightarrow 53(q^2+1)-235q=0$
Đến đây thì ơơn giản rồi.
CM
17 tháng 6 2019
Đáp án A
u 2 − u 3 + u 5 = 10 u 4 + u 6 = 26 ⇒ u 1 + 3 d = 10 2 u 1 + 8 d = 26 ⇒ u 1 = 1 d = 3 ⇒ S = 2023736
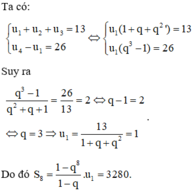
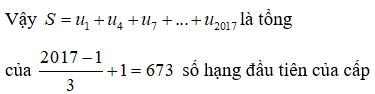
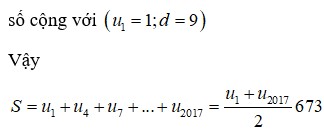
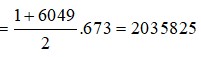
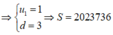
\(\left\{{}\begin{matrix}u1+u2+u3=13\\u4-u1=26\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}u_1+u_1\cdot q+u_1\cdot q^2=13\\u_1\cdot q^3-u_1=26\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}u_1\left(1+q+q^2\right)=13\\u_1\left(q^3-1\right)=26\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\dfrac{1+q+q^2}{\left(q-1\right)\left(q^2+q+1\right)}=\dfrac{13}{26}=\dfrac{1}{2}\\u_1\left(q^3-1\right)=26\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\dfrac{1}{q-1}=\dfrac{1}{2}\\u_1\left(q^3-1\right)=26\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}q-1=2\\u_1=\dfrac{26}{q^3-1}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}q=2+1=3\\u_1=\dfrac{26}{3^3-1}=1\end{matrix}\right.\)
Tổng 8 số hạng đầu của cấp số nhân là:
\(\dfrac{u_1\left(1-q^8\right)}{1-q}=\dfrac{1\cdot\left(1-3^8\right)}{1-3}=3280\)
\(\left\{{}\begin{matrix}u_1+u_2+u_3=13\\u_4-u_1=26\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}u_1+u_1.q+u_1.q^2=13\\u_1.q^3-u_1=26\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}u_1\left(1+q+q^2\right)=13\\u_1\left(q^3-1\right)=26\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}u_1\left(1+q+q^2\right)=13\\u_1\left(q-1\right)\left(q^2+q+1\right)=26\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}13.\left(q-1\right)=26\\u_1.\left(q^3-1\right)=26\end{matrix}\right.\\ \Rightarrow\left\{{}\begin{matrix}q=3\\u_1=1\end{matrix}\right.\)
\(S_8=\dfrac{u_1\left(1-q^8\right)}{1-q}=\dfrac{1.\left(1-3^8\right)}{1-3}=3280\)