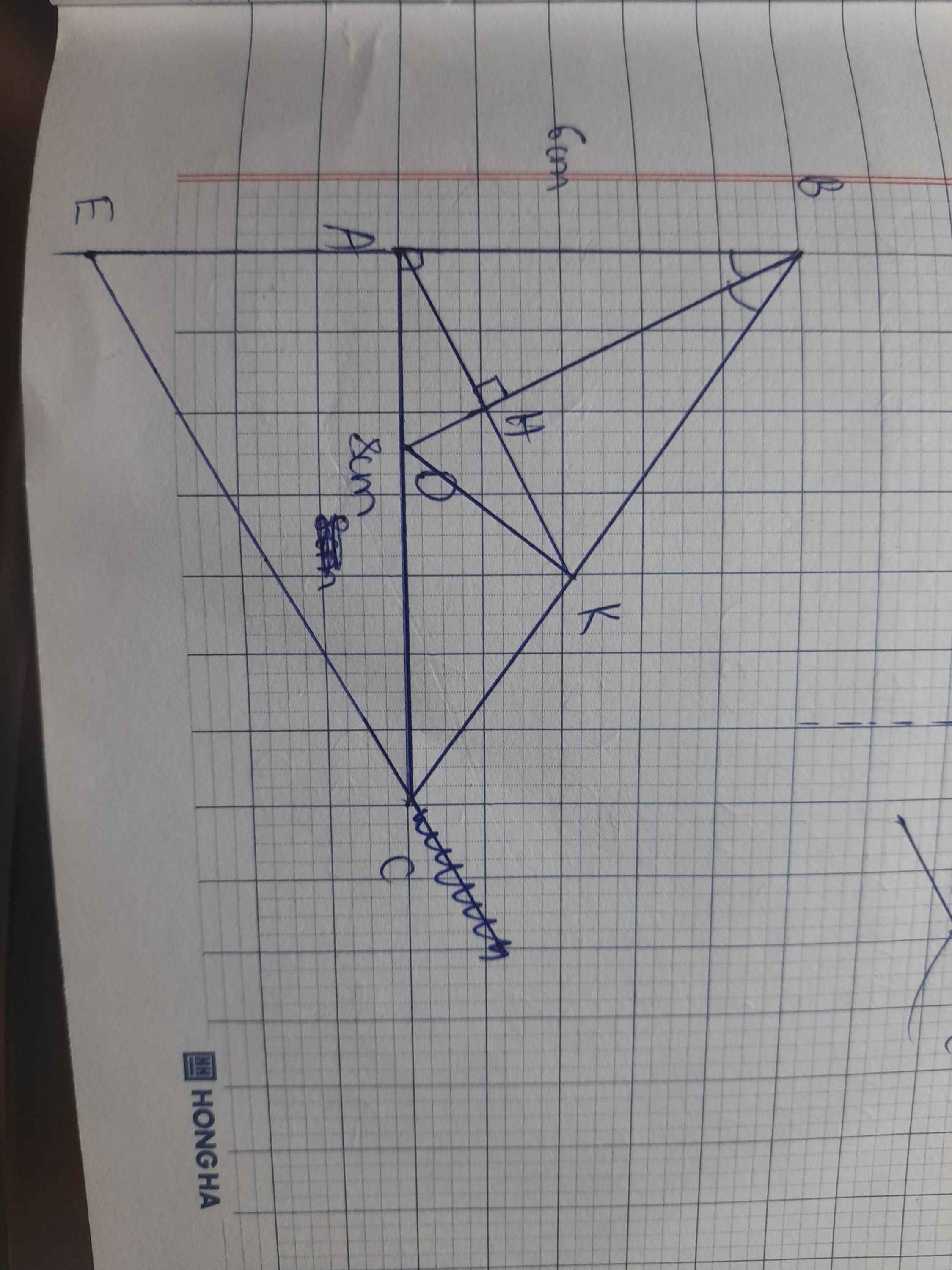
Cho ABC vuông tại A, Biết AB 6cm, AC 8cm . Vẽ đường tròn O đường kính
AB cắt BC tại H.
a) Tính AH, CH.
b) Kẻ OK AH tại K và tia OK cắt AC tại D. Chứng minh DH OH
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(a,\widehat{DHF}=90^0\)(góc nt chắn nửa đg tròn) nên \(DH\perp EF\)
\(b,\left\{{}\begin{matrix}OK\perp HF\\DH\perp HF\end{matrix}\right.\Rightarrow OK//DH;FO=OD\Rightarrow FK=HK\\ \left\{{}\begin{matrix}FO=OD\\FK=HK\end{matrix}\right.\Rightarrow OK.là.đtb.\Delta DFH\)
Lại có \(FD=2FO=10\left(cm\right);DH=\sqrt{FD^2-FH^2}=6\left(cm\right)\left(pytago\right)\)
\(\Rightarrow OK=\dfrac{1}{2}DH=3\left(cm\right)\)
\(c,\) Áp dụng HTL tam giác
\(\Rightarrow DH^2=HE\cdot HF\)
Mà \(2OK=DH\Rightarrow\left(2OK\right)^2=HE\cdot HF\Rightarrow4OK^2=HE\cdot HF\)

Ta có :O là trung điểm của BC(gt)
O là trung điểm của AK(OA=OK)
=>ABKC là hình bình hành(dhnb)
Mà góc BAC = 90 độ
=>ABKC là hình chữ nhật (dhnb)
=>AB=CK và góc ACK = 90 độ
Xét tam giác ABC và tam giác CKA có:
AB=CK(cmt)
góc BAC=góc KCA( cùng bằng 90 độ)
AC chung
Vậy tam giác ABC = tam giác CKA(c.g.c)
b)Xét tam giác AHB và tam giác CHA có
góc AHB = góc CHA (=90 độ)
góc BAH =góc ACH(cùng phụ với góc B)
Vậy tam giác AHB đồng dạng tam giác CHA(g.g)
=>\(\dfrac{AB}{AH}=\dfrac{AC}{CH}\)(1)
Ta có AH\(\perp\)CH
ED\(\perp\)CH
=>AH//DE
Xét tam giác ACH có
AH//DE
=>\(\dfrac{AE}{HD}=\dfrac{AC}{CH}\)
=>\(\dfrac{AE}{AH}=\dfrac{AC}{CH}\)(do AH=AD)(2)
Từ(1) và (2) => \(\dfrac{AB}{AH}=\dfrac{AE}{AH}\)
=>AB=AE(đpcm)

a: BC=căn 6^2+8^2=10cm
AH=6*8/10=4,8cm
c:
Xét tứ giác ANHM có
góc ANH=góc AMH=góc MAN=90 độ
=>ANHM là hình chữ nhật
AD vuông góc MN
=>góc DAC+góc ANM=90 độ
=>góc DAC+góc AHM=90 độ
=>góc DAC+góc ABC=90 độ
=>góc DAC=góc DCA
=>DA=DC
góc DAC+góc DAB=90 độ
góc DCA+góc DBA=90 độ
mà góc DAC=góc DCA
nên góc DAB=góc DBA
=>DA=DB
=>DB=DC
=>D là trung điểm của BC
a: Xét (O) có
ΔAHB nội tiếp
AB là đường kính
Do đó: ΔAHB vuông tại H
=>AH\(\perp\)BC tại H
ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(BC^2=6^2+8^2=100\)
=>\(BC=\sqrt{100}=10\left(cm\right)\)
Xét ΔABC vuông tại A có AH là đường cao
nên \(\left\{{}\begin{matrix}AH\cdot BC=AB\cdot AC\\CA^2=CH\cdot CB\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}AH=\dfrac{6\cdot8}{10}=4,8\left(cm\right)\\CH=\dfrac{8^2}{10}=6,4\left(cm\right)\end{matrix}\right.\)
b: ΔOAH cân tại O
mà OK là đường cao
nên OK là phân giác của \(\widehat{AOH}\)
Xét ΔOAD và ΔOHD có
OA=OH
\(\widehat{AOD}=\widehat{HOD}\)
OD chung
Do đó: ΔOAD=ΔOHD
=>\(\widehat{OAD}=\widehat{OHD}=90^0\)
=>HD\(\perp\)HO