Cho dãy số hữu hạn gồm 10 số hạng, có dạng khai triển là 2,3,5,7,11,...,29. Tính u8.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Số hạng đầu của khai triển là u1 = u(1) = 13 = 1.
Số hạng cuối của khai triển là u5 = u(5) = 53 = 125.
Dãy số được viết dưới dạng khai triển là: 1; 8; 27; 64; 125.

a) Ta có số hạng tổng quát của dãy số \({u_n} = 5n + 1\;\left( {n\; \in {N^*}} \right)\).
b) Các số hạng của dãy số là: 6; 11; 16; 21; 26.
Số hạng đầu của dãy số là: 6 và số hạng cuối của dãy số là 26.

a) Năm số hạng đầu của dãy số là: \(u_1=1^2=1;u_2=2^2=4;u_3=3^2=9;u_4=4^2=16;u_5=5^2=25\).
Số hạng tổng quát của dãy số un là \(u_n=n^2\) với n ∈ ℕ.
b) Dạng khai triển của dãy số \(u_1=1,u_2=4,u_3=9,u_4=16,...u_n=n^2\) ...

a) Số sau hơn số trước 4 dơn vị
b) B={1;5;9;13;17;21;25;29;33;37}

a: Dãy trên có (86-8)/3+2=78/3+2=28(số)
Tổng là (86+3)*28/2=89*14=1246
b: 32 chia 3 dư 2
=>32 thuộc dãy
47 chia 3 dư 2
=>47 thuộc dãy
54 chia hết cho 3
=>54 không thuộc dãy
c: Số thứ 2011 là u1+2010d=8+2010*3=6038

a/
quy luật là mỗi số tiếp theo tăng lên 4 đơn vị
b/
B={ 1;5;9;13;17;21;25;29;33;37}

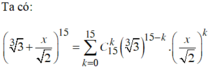
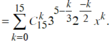
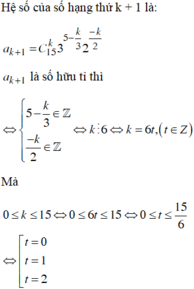


Ta thấy quy luật của dãy này là dãy các số nguyên tố liên tiếp tăng dần. Do đó \(u_8\) chính là số nguyên tố thứ 8 hay \(u_8=19\).